Assessing Assumptions: Independence and Randomness
1 / 31
by Dr. Lucy D'Agostino McGowan
Steps for modeling
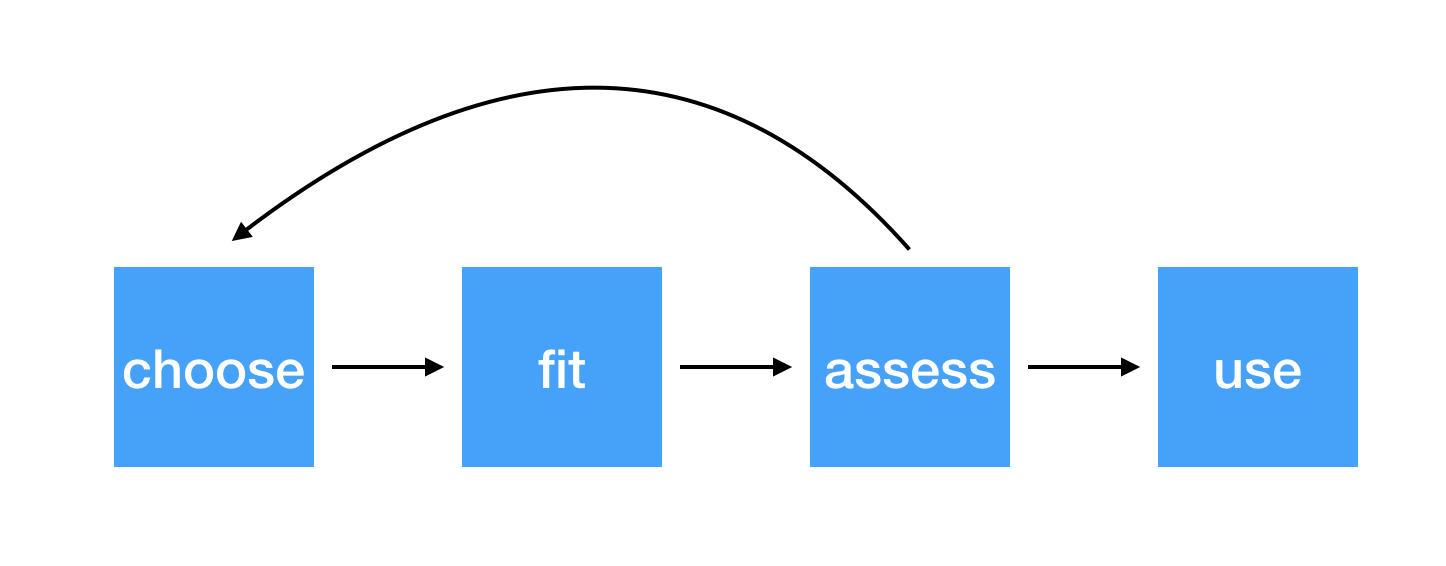
2 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
- Linearity
- Zero Mean
- Constant Variance
- Independence
- Random
- Normality
3 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean |
4 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean | The error distribution is centered at zero | by default | -- |
| Constant Variance |
5 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean | The error distribution is centered at zero | by default | -- |
| Constant Variance | The variability in the errors is the same for all values of the predictor variable | Residuals vs fits plot | fit a better model |
| Independence |
6 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean | The error distribution is centered at zero | by default | -- |
| Constant Variance | The variability in the errors is the same for all values of the predictor variable | Residuals vs fits plot | fit a better model |
| Independence | The errors are assumed to be independent from one another | 👀 data generation | Find better data or fit a fancier model |
| Random |
7 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean | The error distribution is centered at zero | by default | -- |
| Constant Variance | The variability in the errors is the same for all values of the predictor variable | Residuals vs fits plot | fit a better model |
| Independence | The errors are assumed to be independent from one another | 👀 data generation | Find better data or fit a fancier model |
| Random | The data are obtained using a random process | 👀 data generation | Find better data or fit a fancier model |
| Normality |
8 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for ordinary linear regression
| Assumption | What it means | How do you check? | How do you fix? |
|---|---|---|---|
| Linearity | The relationship between the outcome and explanatory variable or predictor is linear holding all other variables constant | Residuals vs. fits plot | fit a better model (transformations, polynomial terms, more / different variables, etc.) |
| Zero Mean | The error distribution is centered at zero | by default | -- |
| Constant Variance | The variability in the errors is the same for all values of the predictor variable | Residuals vs fits plot | fit a better model |
| Independence | The errors are assumed to be independent from one another | 👀 data generation | Find better data or fit a fancier model |
| Random | The data are obtained using a random process | 👀 data generation | Find better data or fit a fancier model |
| Normality | The random errors follow a normal distribution | QQ-plot / residual histogram | fit a better model |
9 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for logistic regression
- Linearity
- Independence
- Randomness
10 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for logistic regression
How do we test linearity?
- Linearity
- Independence
- Randomness
11 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for logistic regression
How do we test linearity?
- Linearity ✅ Plot the empirical logits
- Independence
- Randomness
12 / 31
by Dr. Lucy D'Agostino McGowan
⛳ Testing for linearity in logistic regression
- We can plot the empirical logit to examine the linearity assumption
| Length | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| Number of successes | 84 | 88 | 61 | 61 | 44 |
| Number of failures | 17 | 31 | 47 | 64 | 90 |
| Total | 101 | 119 | 108 | 125 | 134 |
| Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328 |
| Odds of success | 4.941 | 2.839 | 1.298 | 0.953 | 0.489 |
| Empirical logit | 1.60 | 1.04 | 0.26 | −0.05 | −0.72 |
13 / 31
by Dr. Lucy D'Agostino McGowan
⛳ Testing for linearity in logistic regression
data <- data.frame( length = c(3, 4, 5, 6, 7), emp_logit = c(1.6, 1.04, 0.26, -0.05, -0.72))ggplot(data, aes(length, emp_logit)) + geom_point() + geom_abline(intercept = 3.26, slope = -0.566, lty = 2) + labs(y = "log odds of success")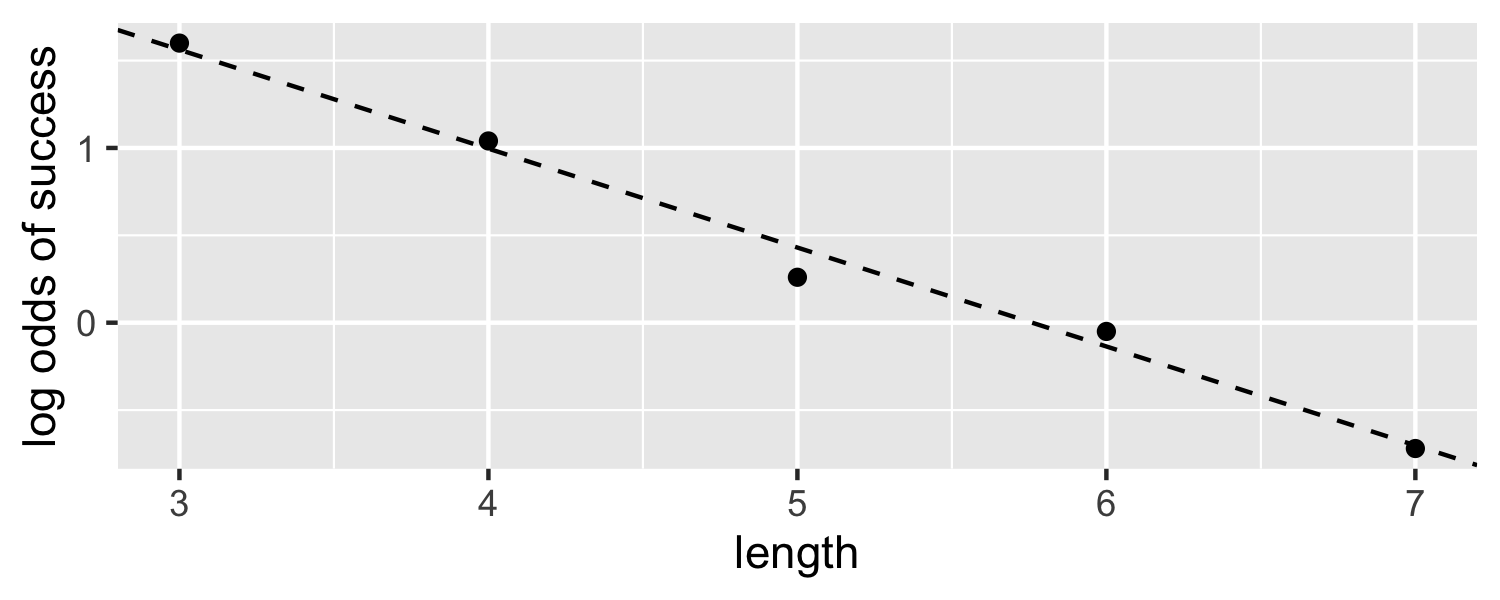
14 / 31
by Dr. Lucy D'Agostino McGowan
Conditions for logistic regression
- Linearity
- Independence
- Randomness
15 / 31
by Dr. Lucy D'Agostino McGowan
Why do we care?
16 / 31
by Dr. Lucy D'Agostino McGowan
Why do we care?
17 / 31
by Dr. Lucy D'Agostino McGowan
Why do we care?
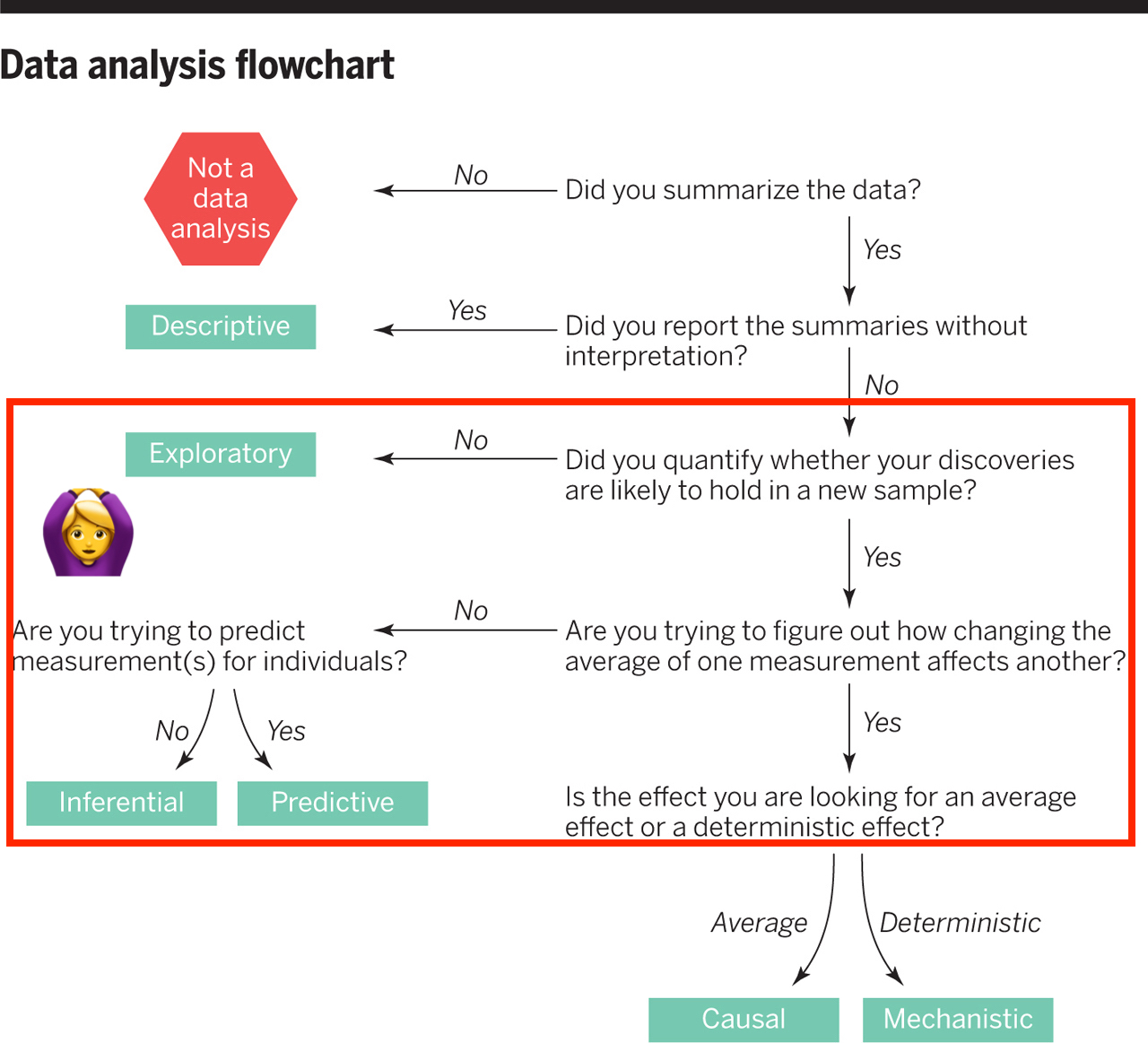
18 / 31
by Dr. Lucy D'Agostino McGowan
Why do we care?
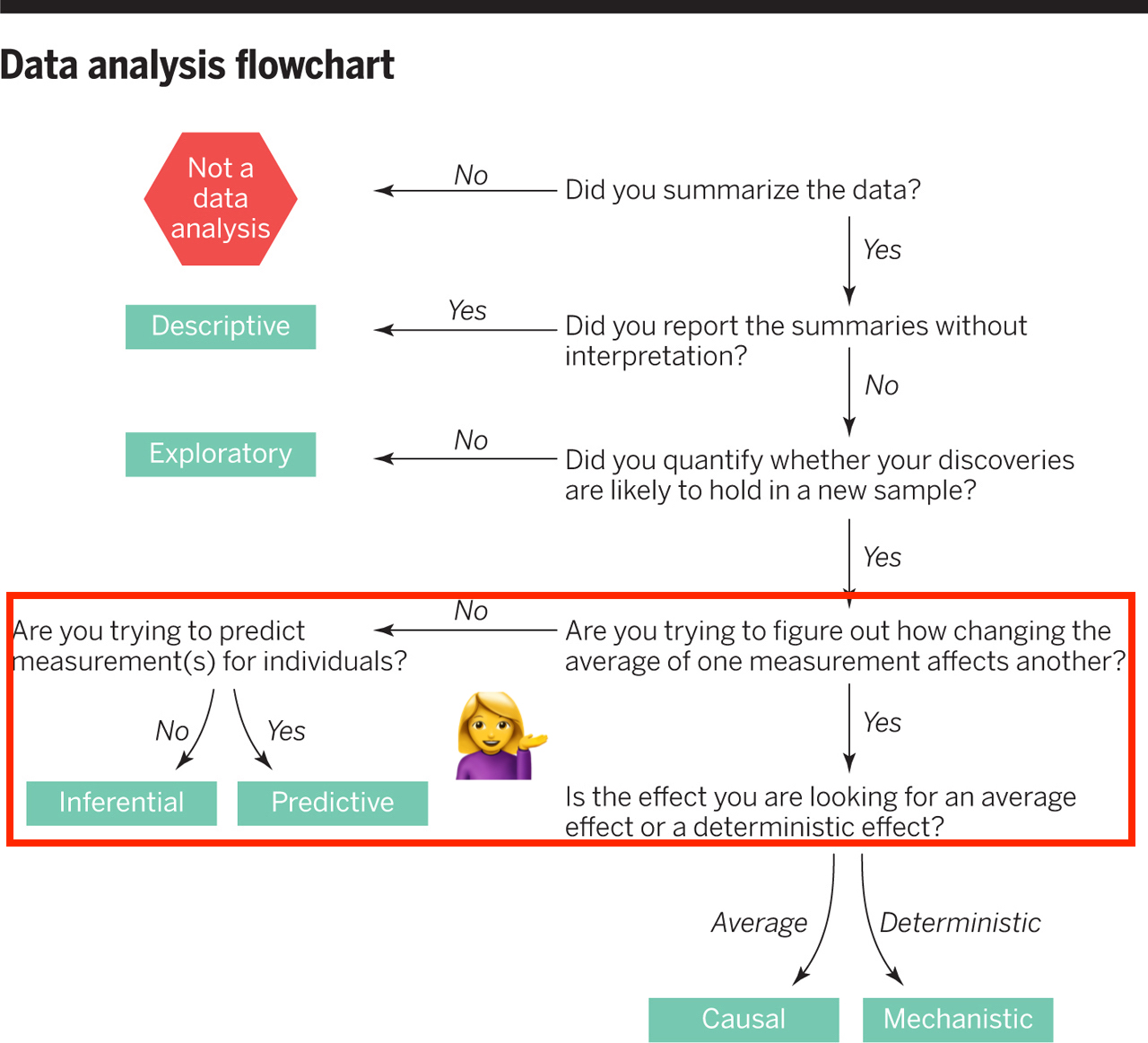
19 / 31
by Dr. Lucy D'Agostino McGowan
Independence
- The observations should be independent of one another
- In the Medical School Admission - GPA example, 55 students were randomly selected and their admission status and GPA were recorded: 👍 Independent or 👎 Not?
20 / 31
by Dr. Lucy D'Agostino McGowan
Independence
- The observations should be independent of one another
- In the Medical School Admission - GPA example, 55 students were randomly selected and their admission status and GPA were recorded: 👍 Independent or 👎 Not?
- 👍
20 / 31
by Dr. Lucy D'Agostino McGowan
Independence
- The observations should be independent of one another
- In the Medical School Admission - GPA example, 55 students were randomly selected and their admission status and GPA were recorded: 👍 Independent or 👎 Not?
- 👍
- A new treatment comes out to help with dry eyes. A sample of 25 people get randomized to either treatment or placebo - this creates a dataset of information about 50 eyes. 👍 or 👎
20 / 31
by Dr. Lucy D'Agostino McGowan
Independence
- The observations should be independent of one another
- In the Medical School Admission - GPA example, 55 students were randomly selected and their admission status and GPA were recorded: 👍 Independent or 👎 Not?
- 👍
- A new treatment comes out to help with dry eyes. A sample of 25 people get randomized to either treatment or placebo - this creates a dataset of information about 50 eyes. 👍 or 👎
- 👎
20 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
What do I put for the family argument if I want to fit a logistic regression in R?
glm(am ~ mpg, data = mtcars, family = "---")21 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
What do I put for the family argument if I want to fit a logistic regression in R?
glm(am ~ mpg, data = mtcars, family = "binomial")- The binomial distribution tells you the number of successes in n experiments
22 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
What do I put for the family argument if I want to fit a logistic regression in R?
glm(am ~ mpg, data = mtcars, family = "binomial")- The binomial distribution tells you the number of successes in n experiments
- For the purposes of this class, n will always be 1
22 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
What do I put for the family argument if I want to fit a logistic regression in R?
glm(am ~ mpg, data = mtcars, family = "binomial")- The binomial distribution tells you the number of successes in n experiments
- For the purposes of this class, n will always be 1
- This is special case of the binomial distribution, called the Bernoulli distribution
22 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
What do I put for the family argument if I want to fit a logistic regression in R?
glm(am ~ mpg, data = mtcars, family = "binomial")- The binomial distribution tells you the number of successes in n experiments
- For the purposes of this class, n will always be 1
- This is special case of the binomial distribution, called the Bernoulli distribution
- Why does this matter? R wants you to specify that you are using the
"binomial"family, your book talks about the Bernoulli distribution, I just want to bridge the gap
22 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
23 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- For example, in a fair coin toss, the probability of getting "heads" is 50%
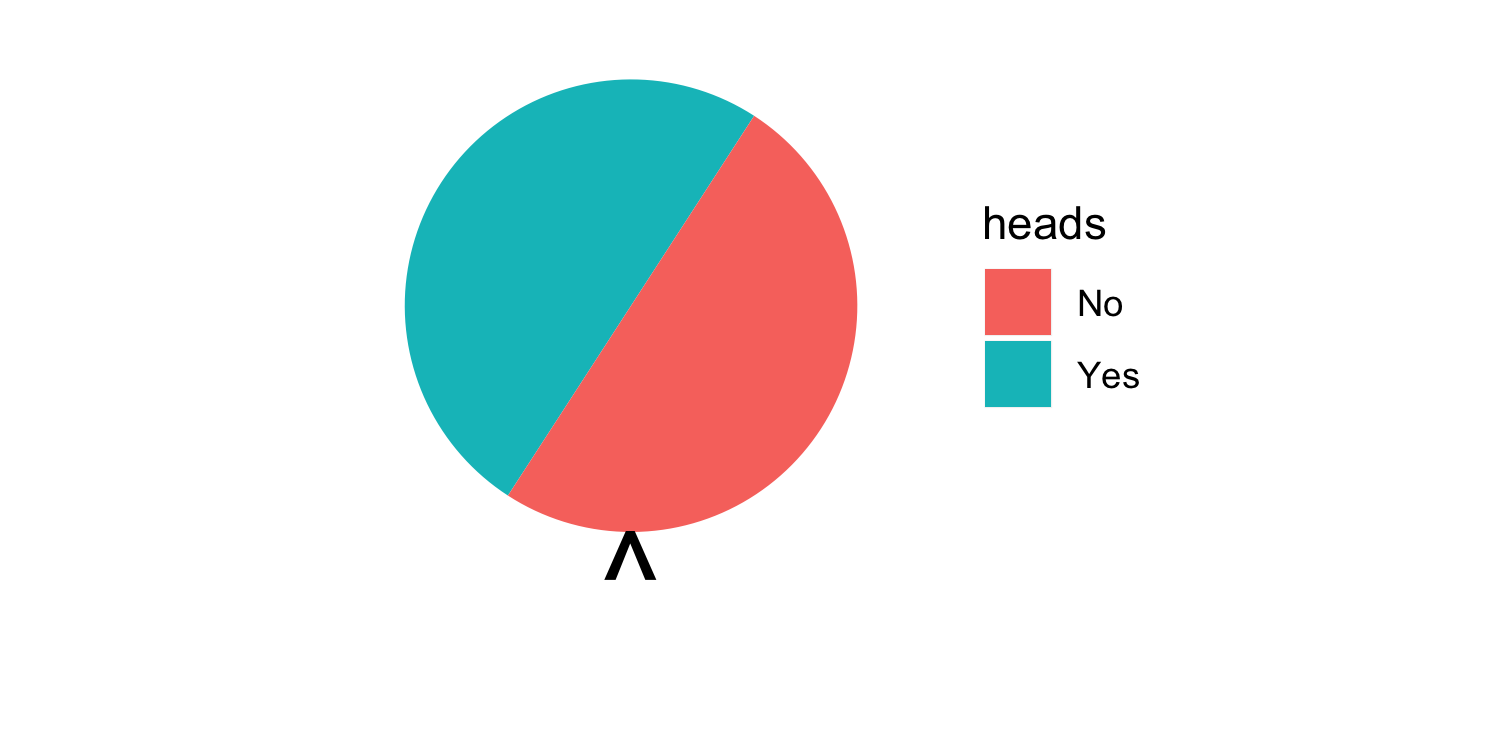
23 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- For example, in a fair coin toss, the probability of getting "heads" is 50%
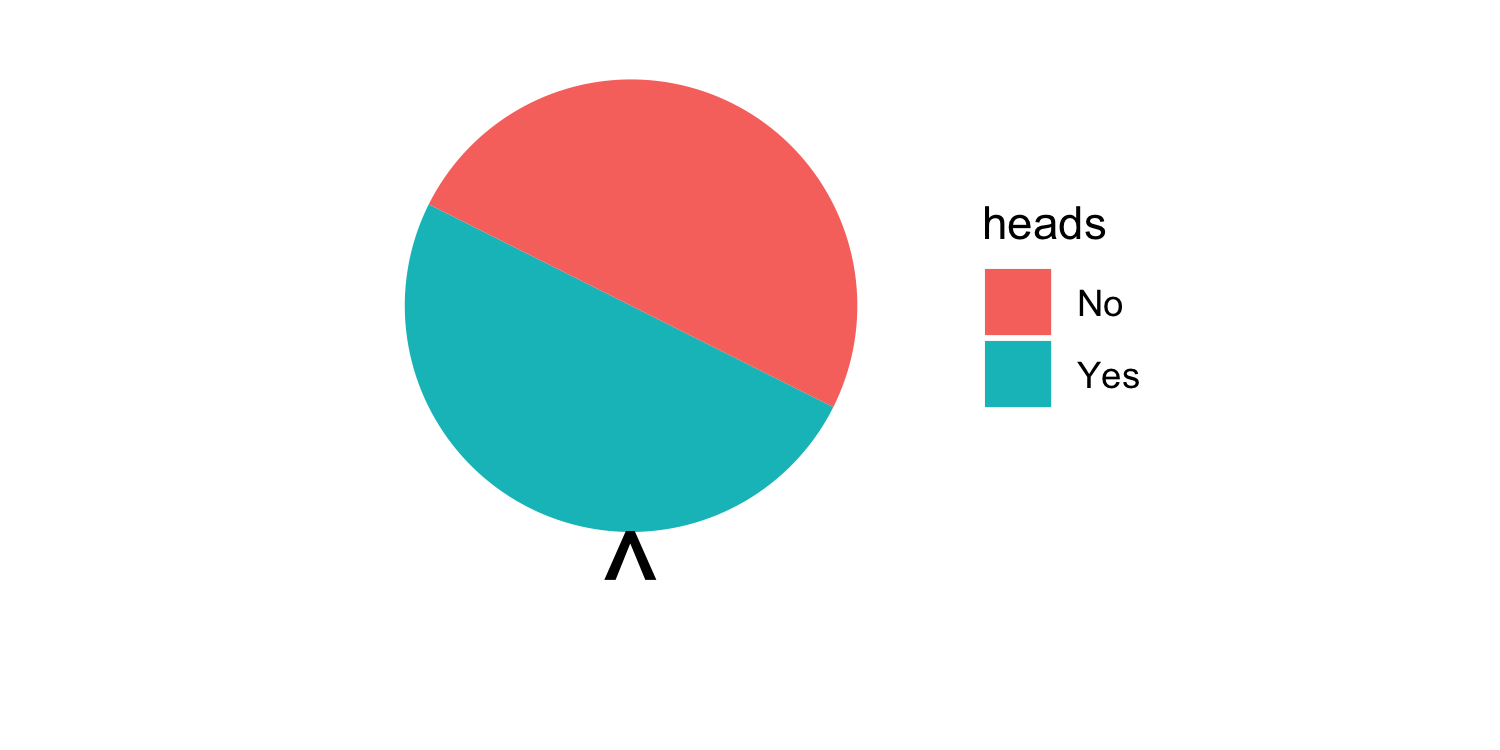
24 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- For example, in a fair coin toss, the probability of getting "heads" is 50%
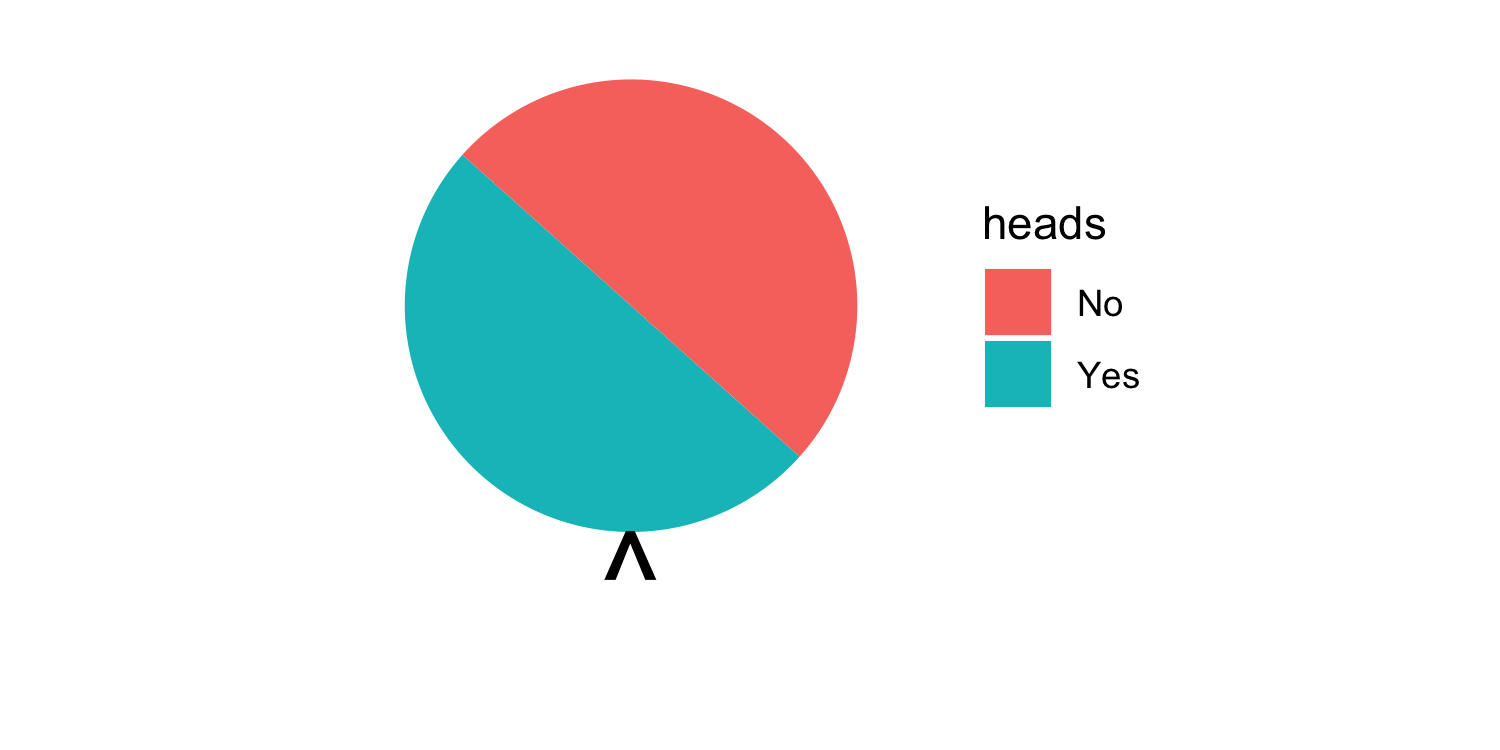
25 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- For example, in a fair coin toss, the probability of getting "heads" is 50%
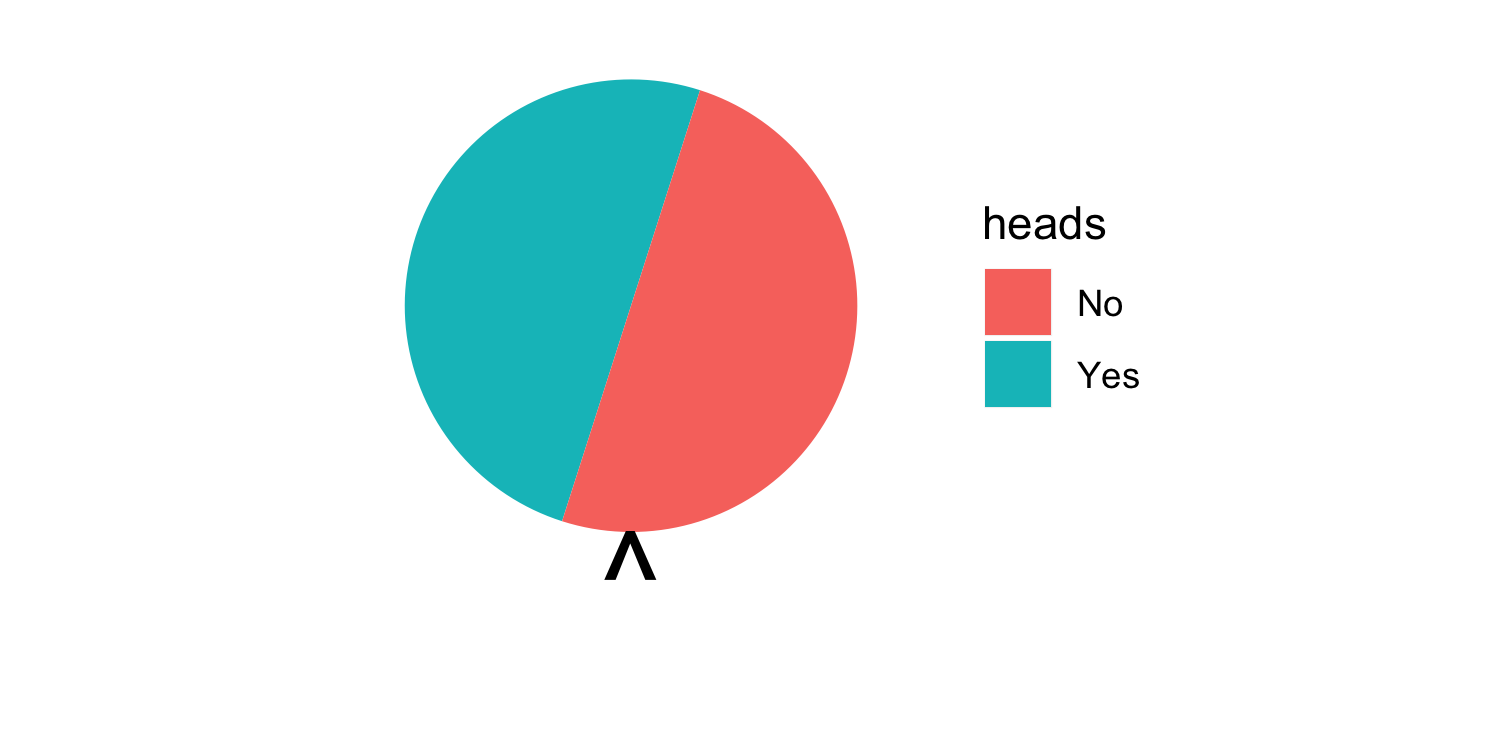
26 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- In the Medical school admissions - GPA example, a student with a 3.8 has an 82% chance of acceptance
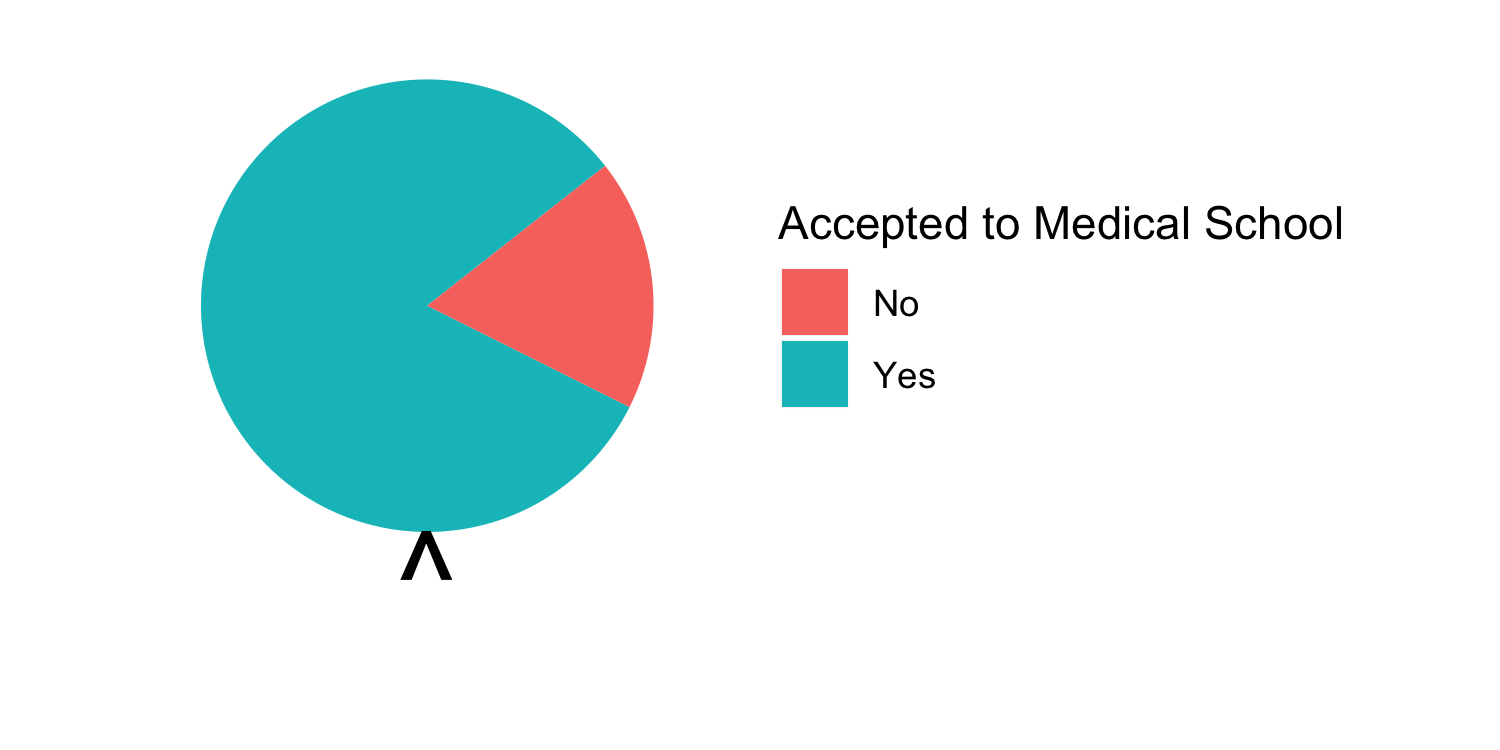
27 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- In the Medical school admissions - GPA example, a student with a 3.8 has an 82% chance of acceptance
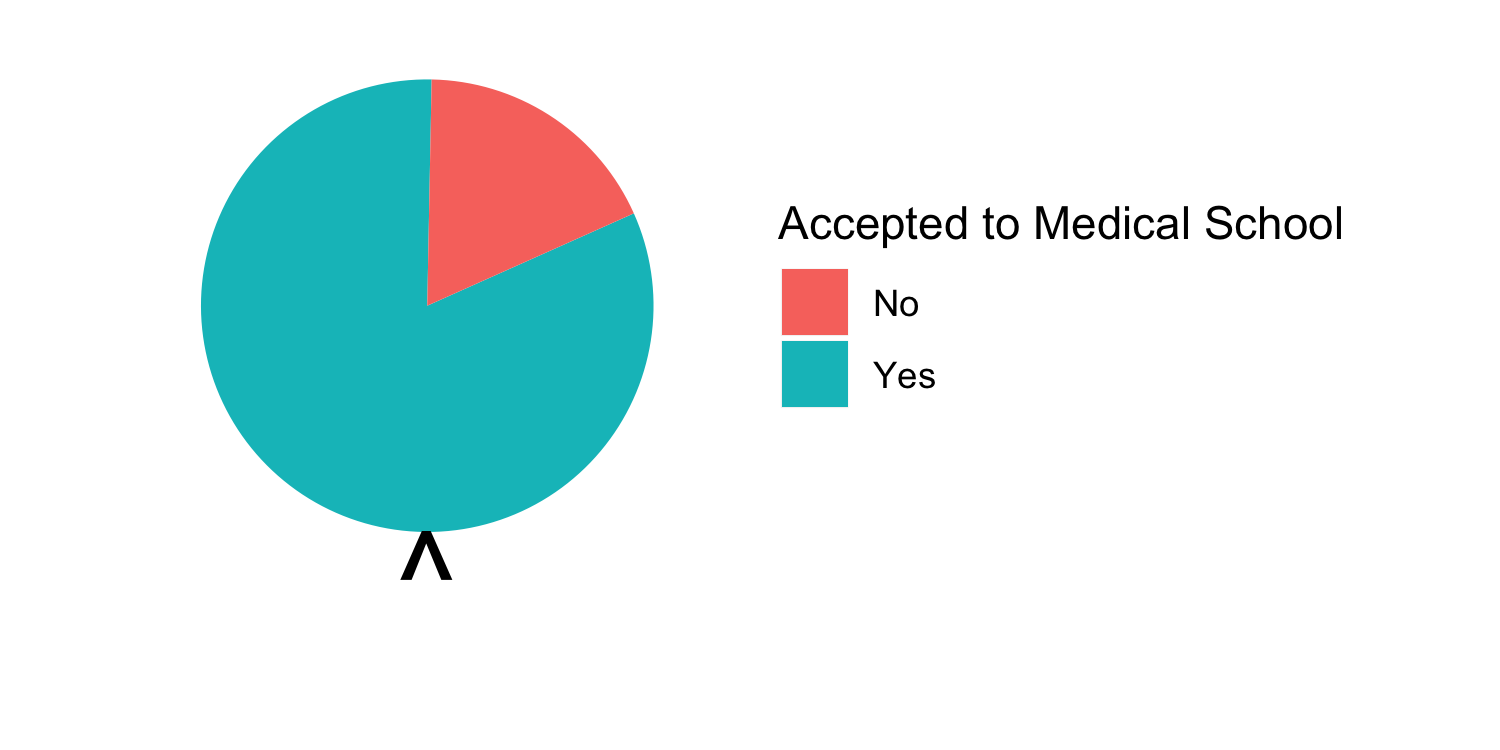
28 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- In the Medical school admissions - GPA example, a student with a 3.8 has an 82% chance of acceptance
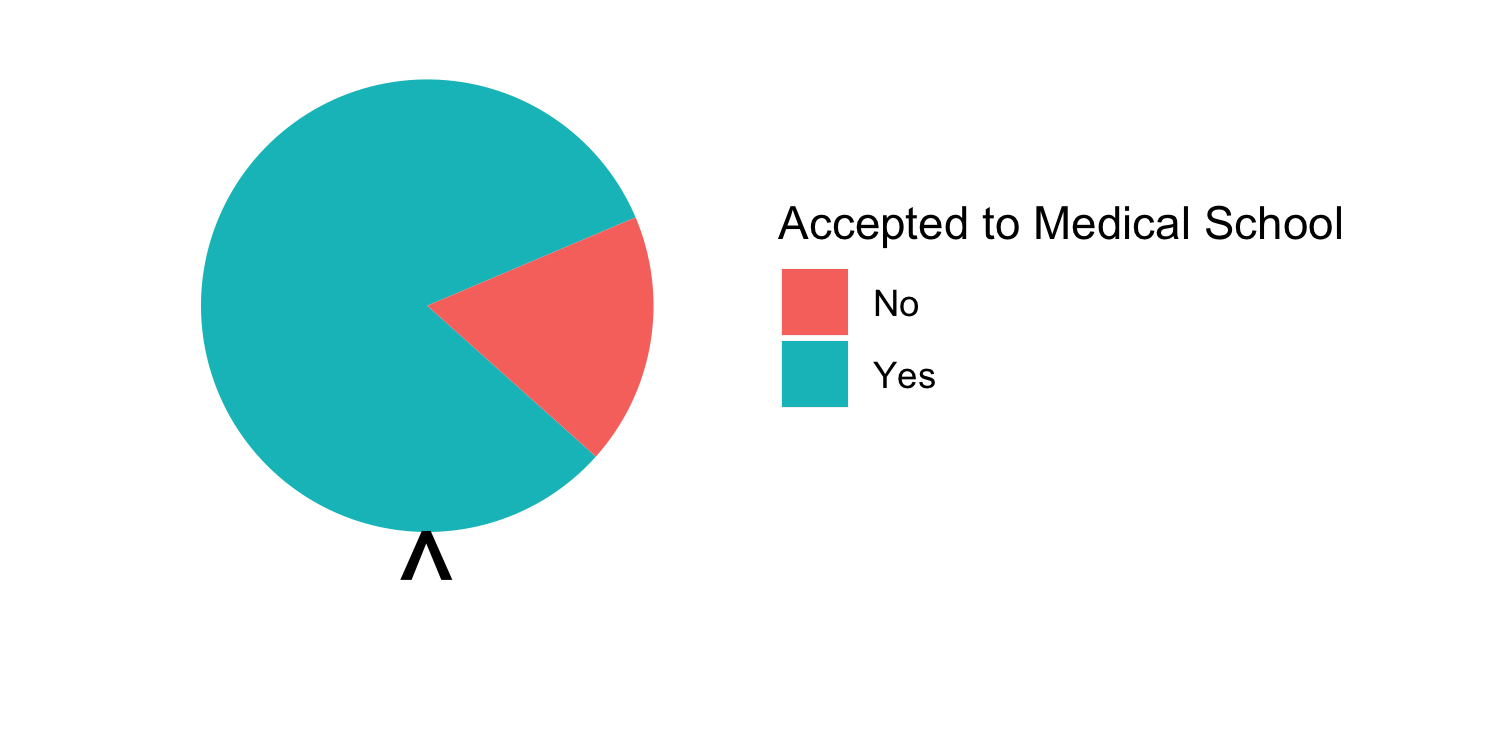
29 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- In the Medical school admissions - GPA example, a student with a 3.8 has an 82% chance of acceptance
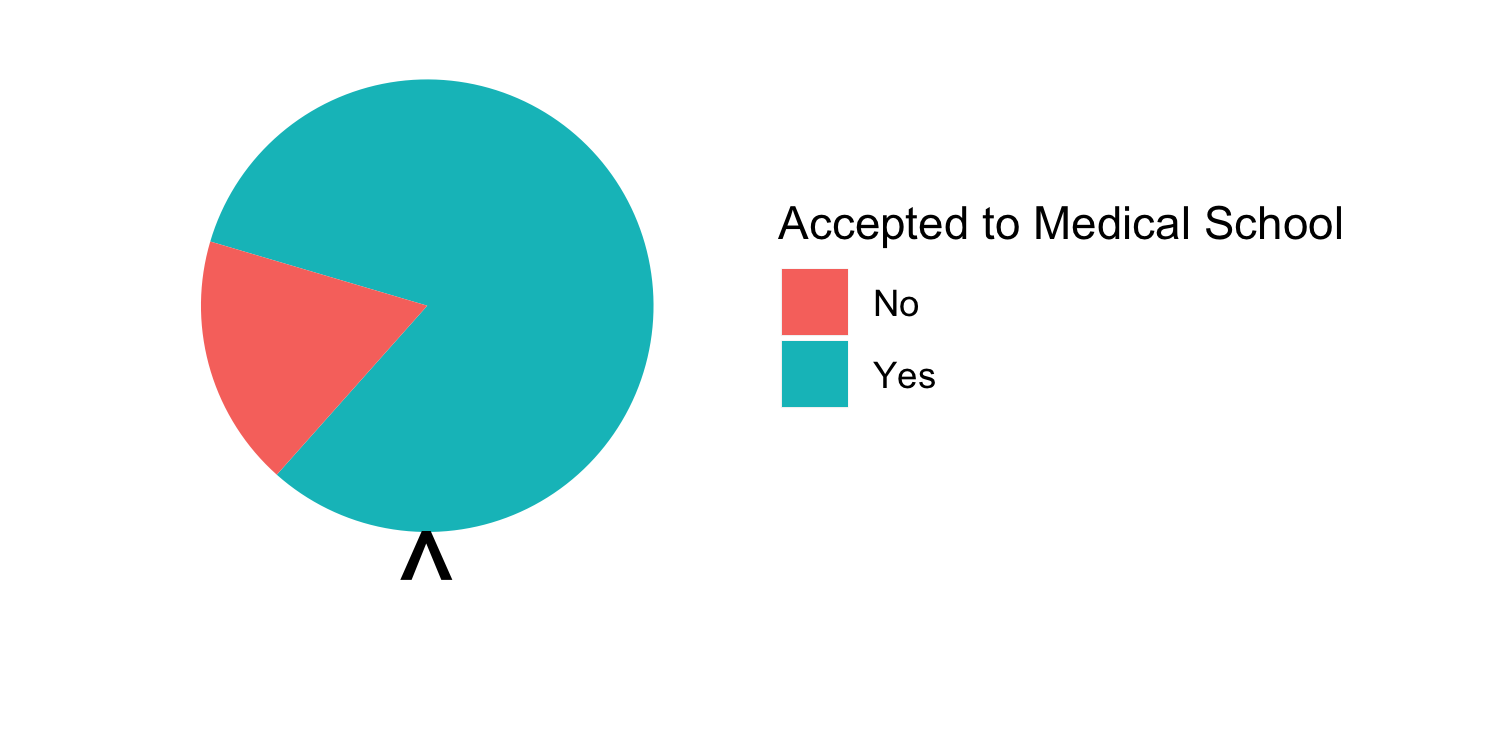
30 / 31
by Dr. Lucy D'Agostino McGowan
Randomness
The Spinner
- A random 0, 1 outcome that behaves like a "spinner" follows the Bernoulli distribution
- In the Medical school admissions - GPA example, a student with a 3.8 has an 82% chance of acceptance
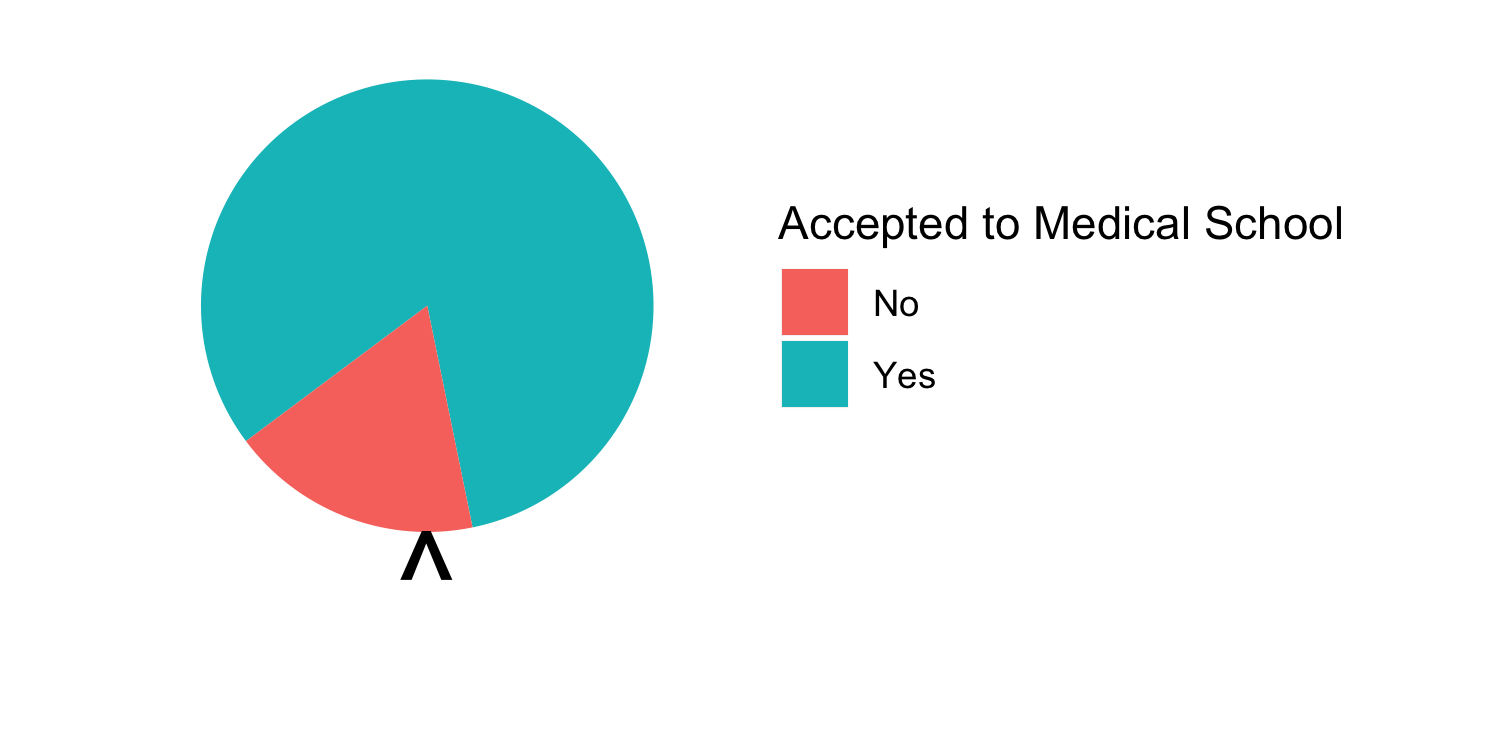
31 / 31