Assessing Logistic Regression

class: center, middle, inverse, title-slide

# Assessing Logistic Regression

---

layout: true

<div class="my-footer">
<span>
by Dr. Lucy D'Agostino McGowan
</span>
</div>

---

# Steps for modeling

![](img/03/flowchart-arrow.png)

---

# Conditions for simple linear regression

* Linearity
* Zero Mean
* Constant Variance
* Independence
* Random
* Normality

---

# Conditions for ~~simple~~ linear regression

* Linearity
* Zero Mean
* Constant Variance
* Independence
* Random
* Normality

---

# Conditions for linear regression

* **Linearity**
* Zero Mean
* Constant Variance
* Independence
* Random
* Normality

---

# Conditions for linear regression

.question[
How do we check these conditions?
]

* Linearity
* Zero Mean
* Constant Variance
* Independence
* Random
* Normality

---

# Conditions for linear regression

.question[
How do we check these conditions?
]

Condition | Graph
------|----
Linearity | Residuals vs. fits
Zero Mean | _by default it's true_
Constant Variance | Residuals vs fits
Independence | No formal check
Random | No formal check
Normality | QQ-plot or histogram of residuals

---

# Conditions for **logistic** regression

* Linearity
* Independence
* Random

---

## Testing linearity for logistic regression

* In logistic regression, the **log(odds)** are a linear function of `\(x\)`, that is: `\(\log(odds) \approx \beta_0 + \beta_1x\)`
* You can check this by plotting the **empirical logits**

--
* Example: ⛳ Examining the relationship between the length of a putt with whether it was made

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134

---

## ⛳ Testing for linearity in logistic regression

.question[
What is the proportion of sucess when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134

---

## ⛳ Testing for linearity in logistic regression

.question[
What is the proportion of sucesses when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328

---

## ⛳ Testing for linearity in logistic regression

.question[
What are the odds of success when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328

---

## ⛳ Testing for linearity in logistic regression

.question[
What are the odds of success when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328
Odds of success | 4.941 | 2.839 | 1.298| 0.953| 0.489

---

## ⛳ Testing for linearity in logistic regression

.question[
What are the log(odds) of success when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328
Odds of success | 4.941 | 2.839 | 1.298| 0.953| 0.489

---

## ⛳ Testing for linearity in logistic regression

.question[
What are the log(odds) of success when length is 3?
]

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328
Odds of success | 4.941 | 2.839 | 1.298| 0.953| 0.489
Empirical logit | 1.60 | 1.04| 0.26 |−0.05 |−0.72

---

## ⛳ Testing for linearity in logistic regression

* We can plot the **empirical logit** to examine the linearity assumption

Length | 3 | 4 | 5 | 6 | 7
------|----|---|---|---|---
Number of successes | 84 | 88 | 61 | 61 | 44 
Number of failures | 17 | 31 | 47 | 64 | 90 
Total | 101 | 119 | 108 | 125 | 134
Probability of success | 0.832 | 0.739 | 0.565 | 0.488 | 0.328
Odds of success | 4.941 | 2.839 | 1.298| 0.953| 0.489
Empirical logit | 1.60 | 1.04| 0.26 |−0.05 |−0.72

---

## ⛳ Testing for linearity in logistic regression

.small[

```r
data <- data.frame(
  length = c(3, 4, 5, 6, 7),
  emp_logit = c(1.6, 1.04, 0.26, -0.05, -0.72)
)
ggplot(data, aes(length, emp_logit)) + 
  geom_point() + 
  labs(y = "log odds of success")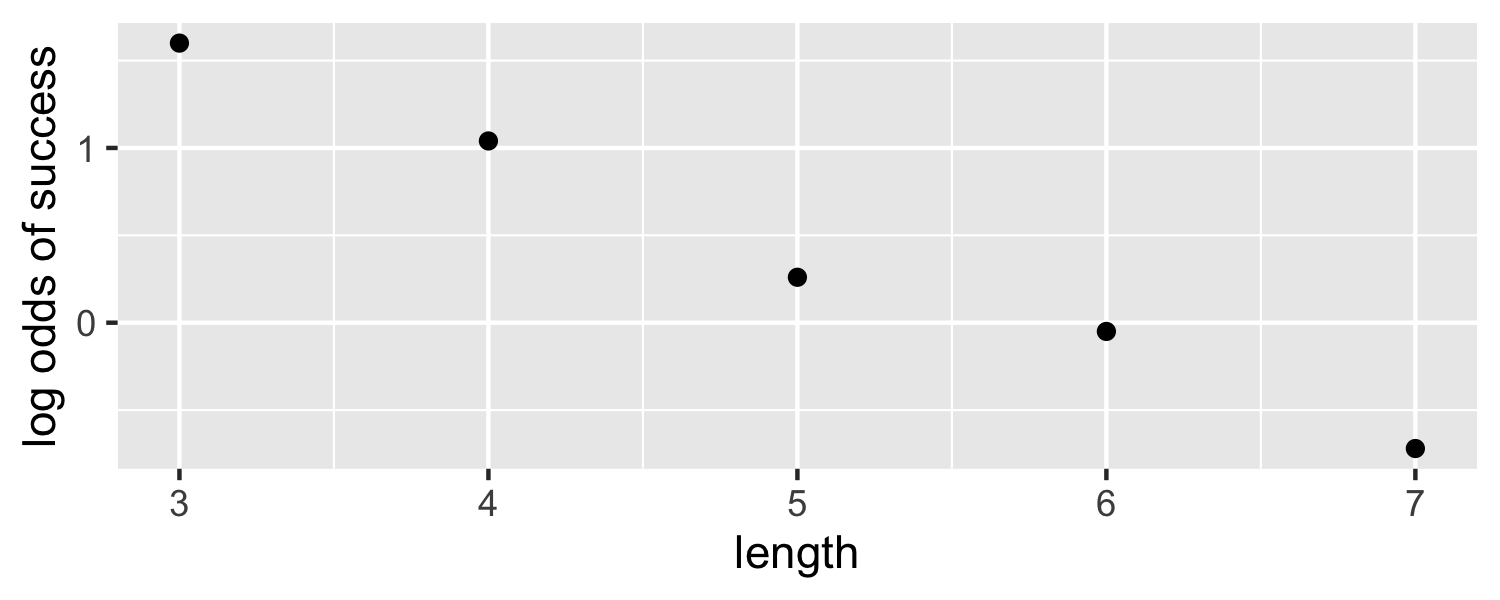
```

![](12-assessing-logistic_files/figure-html/unnamed-chunk-3-1.png)
]

---

## ⛳ Testing for linearity in logistic regression

.small[

```r
data <- data.frame(
  length = c(3, 4, 5, 6, 7),
  emp_logit = c(1.6, 1.04, 0.26, -0.05, -0.72)
)
ggplot(data, aes(length, emp_logit)) + 
  geom_point() + 
  geom_abline(intercept = 3.26, slope = -0.566, lty = 2) +
  labs(y = "log odds of success")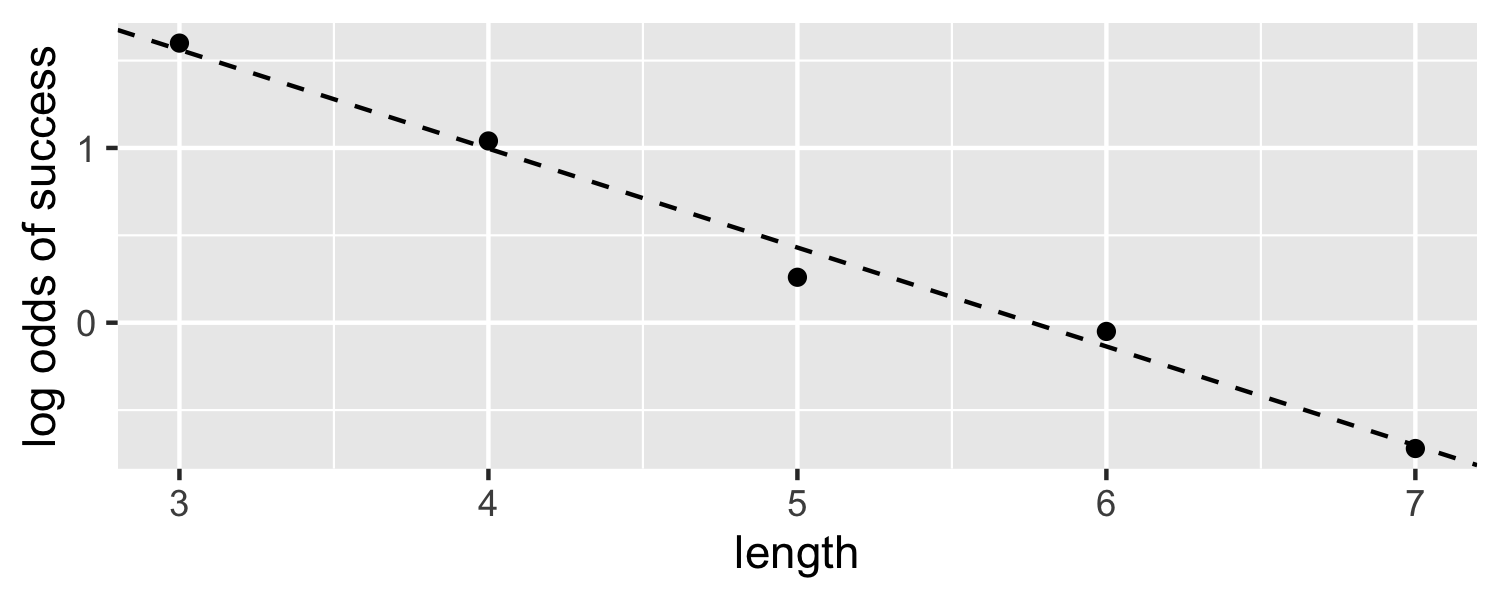
```

![](12-assessing-logistic_files/figure-html/unnamed-chunk-4-1.png)
]

---

##  Testing for linearity in logistic regression

.question[
What if the `\(x\)` variable isn't discrete?
]

* We can plot the **empirical logit** to examine the linearity assumption

--
* You can create "bins" and calculate the empirical logit within each bin (for example, count the number of success when x is between 1 and 5: bin 1, count the number of successes when x is between 5 and 10: bin 2, etc)

---

# Conditions for **logistic** regression

* Linearity ✅
* Independence
* Random

---

# Randomness

* This cannot be formally "checked" via a graph
* You have to think about the data generating process
* Let's look at some examples

---

## Randomness

.question[
Does randomness hold?
]

During the 1970s, when women were entering the workforce in substantial numbers
for the first time since World War II, many men were opposed to the trend. One study
chose a random sample of men and asked them to agree or disagree with the statement
“Women should stay in the home and let men run the country.” A linear logistic regression
relating the proportion of men who agreed to their years of education showed a strong relationship
with a negative slope: The more time a man spent in school, the less likely he was
to agree.

--

* Yes! This was a "random sample"

---

## Randomness

.question[
Does randomness hold?
]

One of the authors of our Stat2Data book tried to apply logistic regression to a bluegrass banjo "roll", an eight-note sequence with a fixed pattern. According to the logistic model, the predictor is the time in the sequence when the note is played (1 to 8) and the response is whether the note is picked with the thumb:

Forward roll:| 1 2 3 4 5 6 7 8
---|---
Thumb? (1 = Yes)| 1 0 0 1 0 0 1 0

--

* No! There is no randomness because the sequence is fixed. Notice that it is possible to
compute p-values and interval estimates. Notice also that a (brainless) computer will do it for
you if you ask.

---

# Conditions for **logistic** regression

* Linearity ✅
* Independence 
* Random ✅

---

# Independence

* Even if outcomes are random, they may not be independent. 
* For example, if you put tickets numbered 1 to 10 in a box, mix them up, and take them out one at a time, the sequence you get is random, but the individual outcomes are not independent.
* If your first ticket is #9, your second cannot be. 
* If you put #9 back and mix again before you grab the next ticket, your outcomes are both random and independent.