Introduction to Logistic Regression
1 / 30
by Dr. Lucy D'Agostino McGowan
what are the odds
- Go to RStudio Cloud and open
what are the odds
2 / 30
by Dr. Lucy D'Agostino McGowan
Outcome variable
- So far, we've only had continuous (numeric, quantitative) outcome variables ( y )
3 / 30
by Dr. Lucy D'Agostino McGowan
Outcome variable
- So far, we've only had continuous (numeric, quantitative) outcome variables ( y )
- We've just learned about categorical and binary explanatory variables ( x )
3 / 30
by Dr. Lucy D'Agostino McGowan
Outcome variable
- So far, we've only had continuous (numeric, quantitative) outcome variables ( y )
- We've just learned about categorical and binary explanatory variables ( x )
- What if we have a binary outcome variable?
3 / 30
by Dr. Lucy D'Agostino McGowan
Outcome variable
What does it mean to be a binary variable?
- So far, we've only had continuous (numeric, quantitative) outcome variables ( y )
- We've just learned about categorical and binary explanatory variables ( x )
- What if we have a binary outcome variable?
4 / 30
by Dr. Lucy D'Agostino McGowan
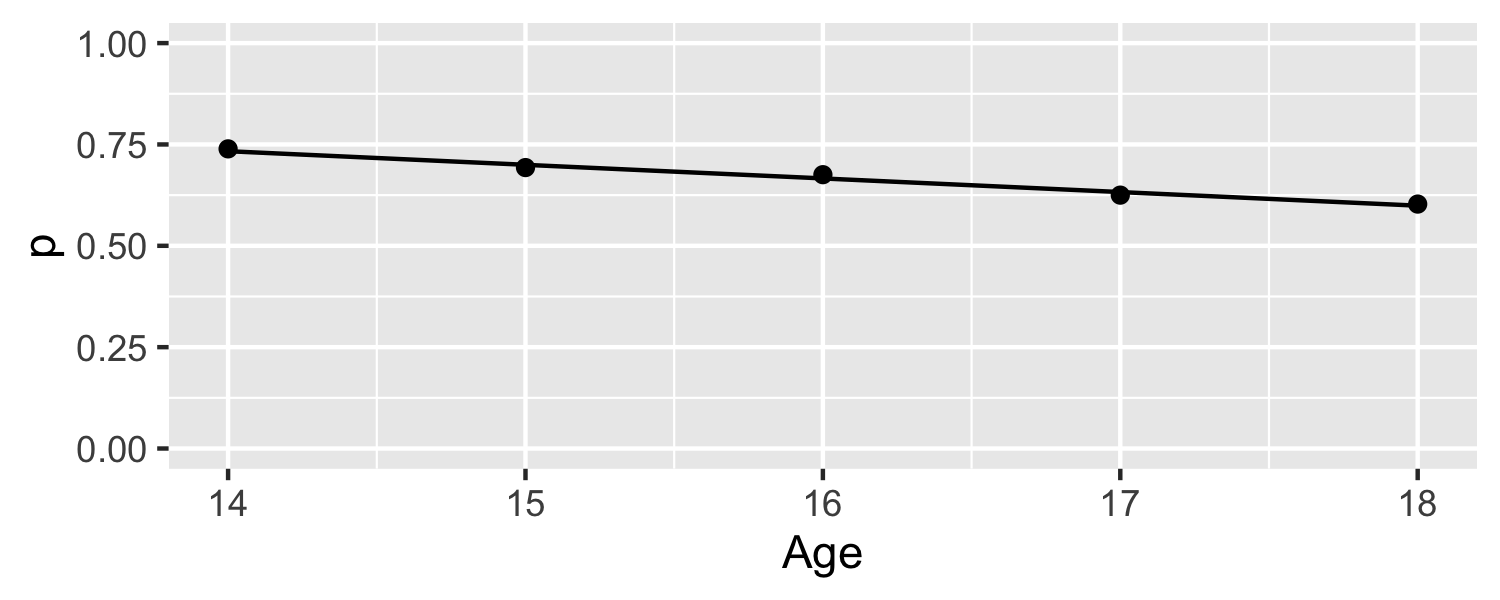
Let's look at an example
- 446 teens were asked "On an average school night, do you get at least 7 hours of sleep"
- Outcome is [1 = "Yes", 0 = "No"]
- Is Age related to this outcome?
5 / 30
by Dr. Lucy D'Agostino McGowan
Let's look at an example
- 446 teens were asked "On an average school night, do you get at least 7 hours of sleep"
- Outcome is [1 = "Yes", 0 = "No"]
- Is Age related to this outcome?
- What if I try to fit this as a linear regression model?
5 / 30
by Dr. Lucy D'Agostino McGowan
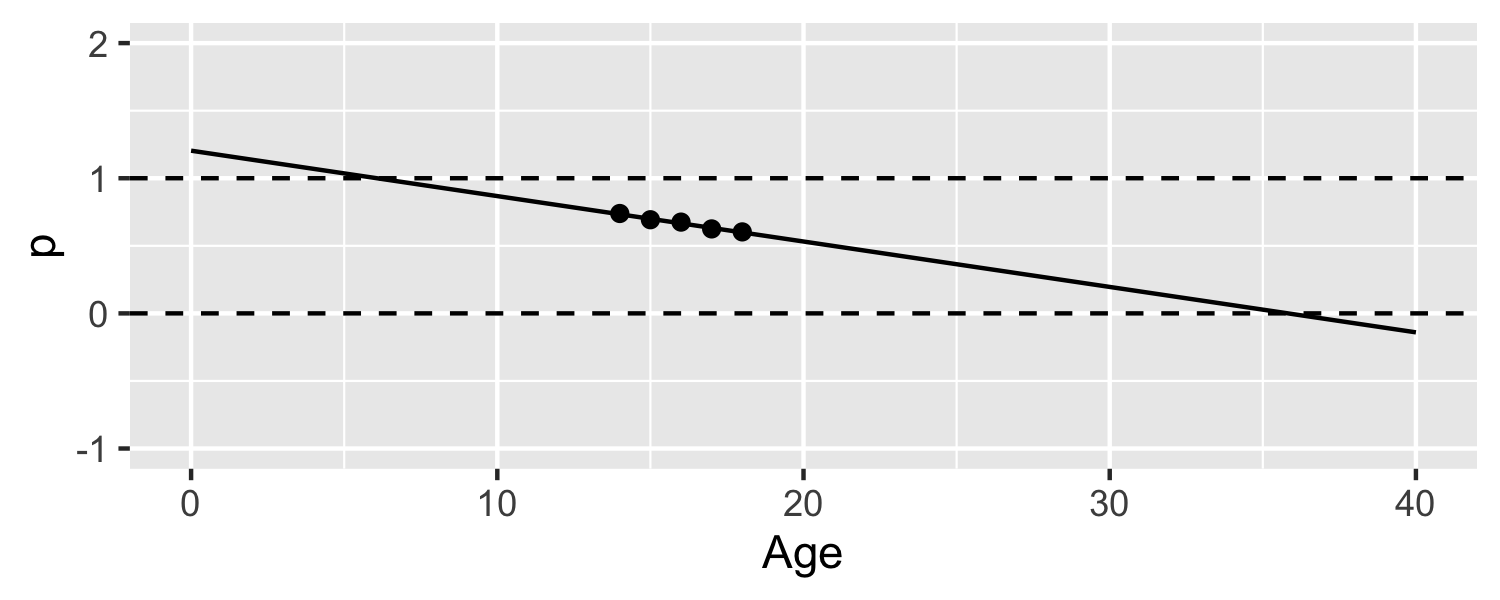
Let's look at an example
- 446 teens were asked "On an average school night, do you get at least 7 hours of sleep"
- Outcome is [1 = "Yes", 0 = "No"]
- Is Age related to this outcome?
- What if I try to fit this as a linear regression model?

5 / 30
by Dr. Lucy D'Agostino McGowan
Let's look at an example
- 446 teens were asked "On an average school night, do you get at least 7 hours of sleep"
- Outcome is [1 = "Yes", 0 = "No"]
- Is Age related to this outcome?
- What if I try to fit this as a linear regression model?
6 / 30
by Dr. Lucy D'Agostino McGowan
Let's look at an example
- 446 teens were asked "On an average school night, do you get at least 7 hours of sleep"
- Outcome is [1 = "Yes", 0 = "No"]
- Is Age related to this outcome?
- What if I try to fit this as a linear regression model?
7 / 30
by Dr. Lucy D'Agostino McGowan
Let's look at an example
- Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
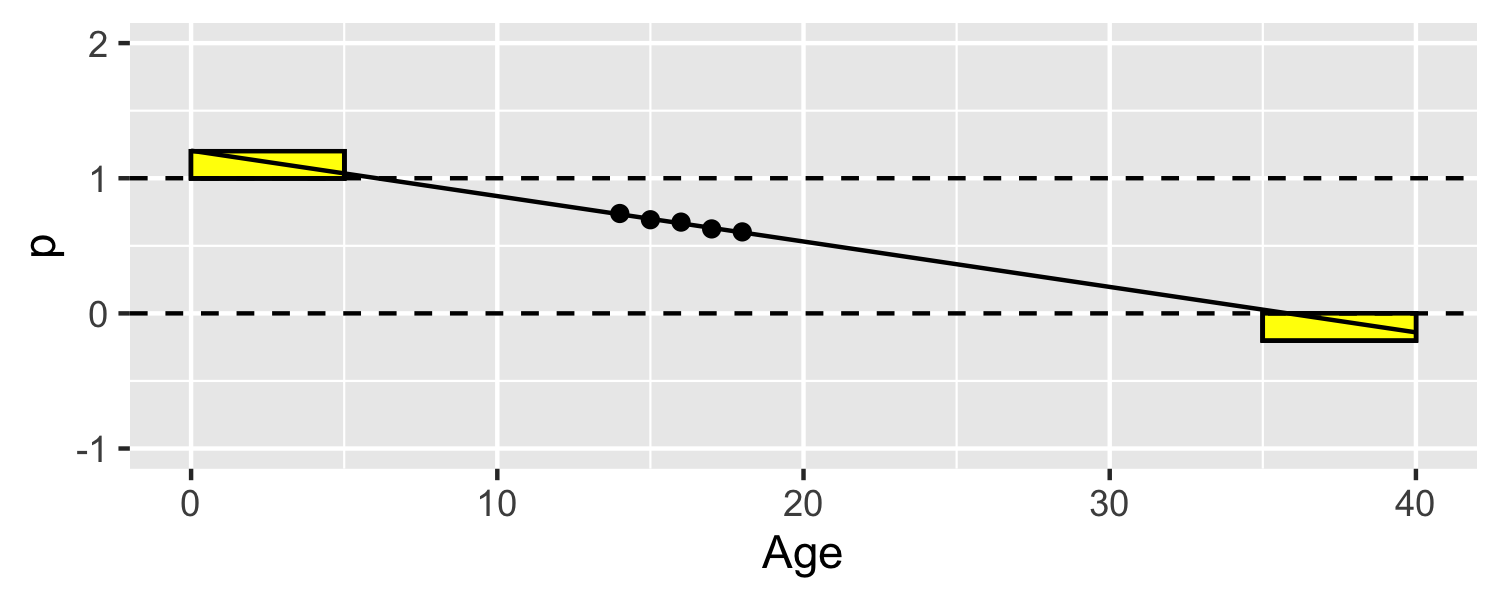
8 / 30
by Dr. Lucy D'Agostino McGowan
Let's look at an example
- Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
9 / 30
by Dr. Lucy D'Agostino McGowan
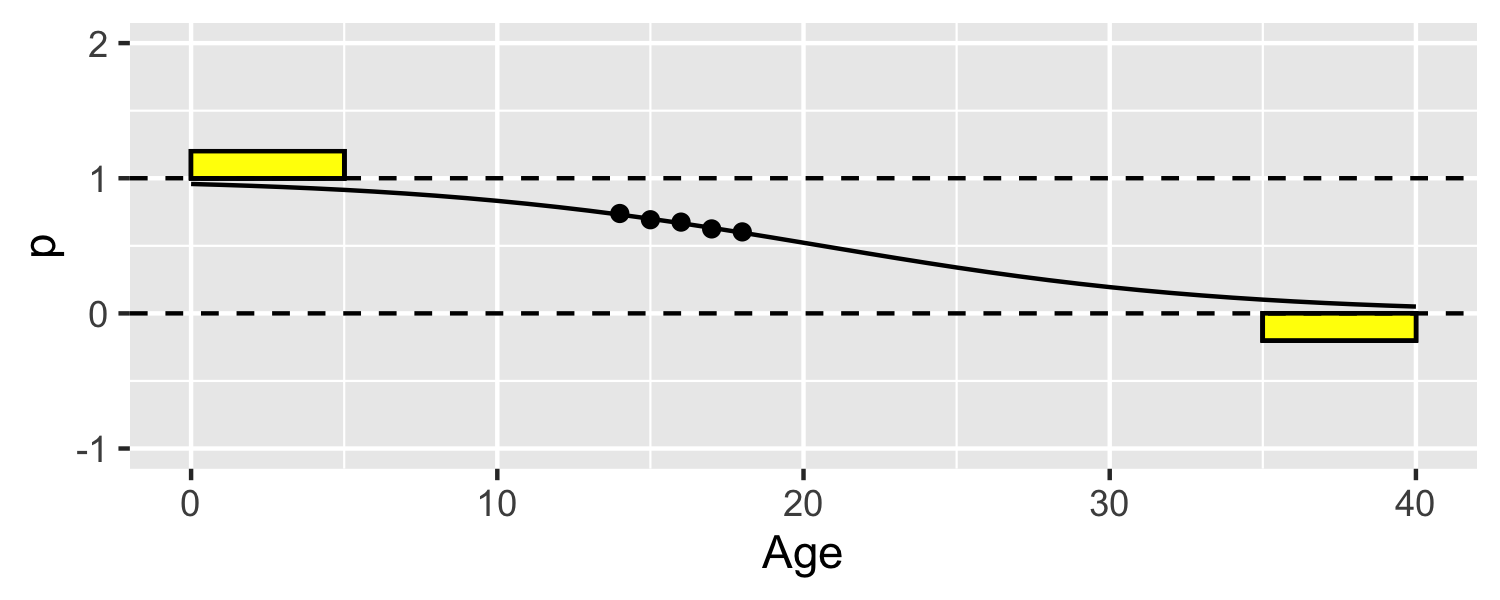
Let's look at an example
- Perhaps it would be sensible to find a function that would not extend beyond 0 and 1?
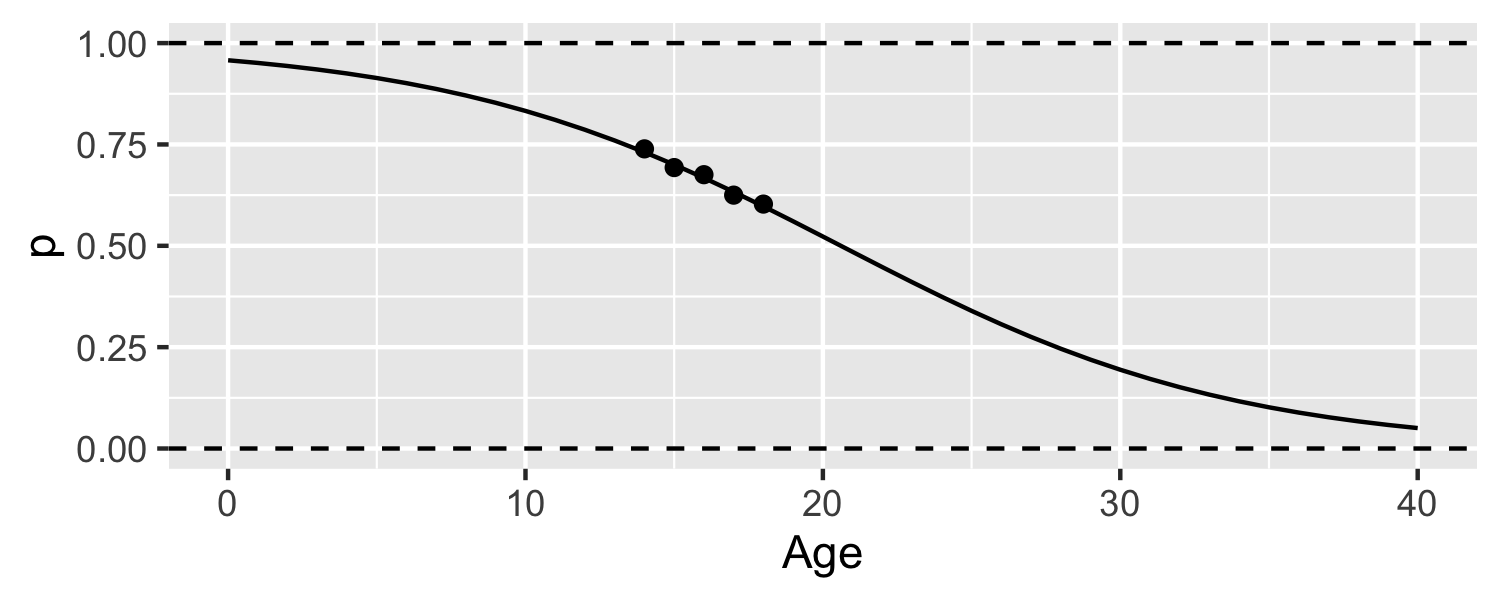
- this line is fit using logistic regression model
10 / 30
by Dr. Lucy D'Agostino McGowan
How does this compare to linear regression?
| Model | Outcome | Form |
|---|---|---|
| Ordinary linear Regression | Numeric | y≈β0+β1x |
| Number of Doctors example | Numeric | √Number of doctors≈β0+β1x |
| Logistic regression | Binary | log(π1−π)≈β0+β1x |
11 / 30
by Dr. Lucy D'Agostino McGowan
How does this compare to linear regression?
| Model | Outcome | Form |
|---|---|---|
| Ordinary linear Regression | Numeric | y≈β0+β1x |
| Number of Doctors example | Numeric | √Number of doctors≈β0+β1x |
| Logistic regression | Binary | log(π1−π)≈β0+β1x |
- π is the probability that y=1 ( P(y=1) )
11 / 30
by Dr. Lucy D'Agostino McGowan
Notation
- log(π1−π): the "log odds"
12 / 30
by Dr. Lucy D'Agostino McGowan
Notation
- log(π1−π): the "log odds"
- π is the probability that y=1 - the probability that your outcome is 1.
12 / 30
by Dr. Lucy D'Agostino McGowan
Notation
- log(π1−π): the "log odds"
- π is the probability that y=1 - the probability that your outcome is 1.
- π1−π is a ratio representing the odds that y=1
12 / 30
by Dr. Lucy D'Agostino McGowan
Notation
- log(π1−π): the "log odds"
- π is the probability that y=1 - the probability that your outcome is 1.
- π1−π is a ratio representing the odds that y=1
- log(π1−π) is the log odds
12 / 30
by Dr. Lucy D'Agostino McGowan
Notation
- log(π1−π): the "log odds"
- π is the probability that y=1 - the probability that your outcome is 1.
- π1−π is a ratio representing the odds that y=1
- log(π1−π) is the log odds
- The transformation from π to log(π1−π) is called the logistic or logit transformation
12 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- 👛 if I flip a fair coin, what is the probability that I'd get heads?
13 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- 👛 if I flip a fair coin, what is the probability that I'd get heads?
- p=0.5
13 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- 👛 if I flip a fair coin, what is the probability that I'd get heads?
- p=0.5
- What is the probability that I'd get tails?
13 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- 👛 if I flip a fair coin, what is the probability that I'd get heads?
- p=0.5
- What is the probability that I'd get tails?
- 1−p=0.5
13 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- 👛 if I flip a fair coin, what is the probability that I'd get heads?
- p=0.5
- What is the probability that I'd get tails?
- 1−p=0.5
- The odds are 1:1, 0.5:0.5
- the odds can be written as p1−p=0.50.5=1
13 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
14 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
- p=0.6
14 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
- p=0.6
- What is the probability that it won't rain?
14 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
- p=0.6
- What is the probability that it won't rain?
- 1−p=0.4
14 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
- p=0.6
- What is the probability that it won't rain?
- 1−p=0.4
- What are the odds that it will rain?
14 / 30
by Dr. Lucy D'Agostino McGowan
A bit about "odds"
- The "odds" tell you how likely an event is
- ☔ Let's say there is a 60% chance of rain today
- What is the probability that it will rain?
- p=0.6
- What is the probability that it won't rain?
- 1−p=0.4
- What are the odds that it will rain?
- 3 to 2, 3:2, 0.60.4=1.5
14 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
- How do you "undo" a log base e?
15 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
- How do you "undo" a log base e?
- Use e! For example:
- elog(10)=10
15 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
- How do you "undo" a log base e?
- Use e! For example:
- elog(10)=10
- elog(1283)=1283
15 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
- How do you "undo" a log base e?
- Use e! For example:
- elog(10)=10
- elog(1283)=1283
- elog(x)=x
15 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
How would you get the odds from the log(odds)?
- How do you "undo" a log base e?
- Use e! For example:
- elog(10)=10
- elog(1283)=1283
- elog(x)=x
16 / 30
by Dr. Lucy D'Agostino McGowan
Transforming logs
How would you get the odds from the log(odds)?
- How do you "undo" a log base e?
- Use e! For example:
- elog(10)=10
- elog(1283)=1283
- elog(x)=x
- elog(odds) = odds
16 / 30
by Dr. Lucy D'Agostino McGowan
Transforming odds
- odds = π1−π
- Solving for π
- π=odds1+odds
17 / 30
by Dr. Lucy D'Agostino McGowan
Transforming odds
- odds = π1−π
- Solving for π
- π=odds1+odds
- Plugging in elog(odds) = odds
17 / 30
by Dr. Lucy D'Agostino McGowan
Transforming odds
- odds = π1−π
- Solving for π
- π=odds1+odds
- Plugging in elog(odds) = odds
- π=elog(odds)1+elog(odds)
17 / 30
by Dr. Lucy D'Agostino McGowan
Transforming odds
- odds = π1−π
- Solving for π
- π=odds1+odds
- Plugging in elog(odds) = odds
- π=elog(odds)1+elog(odds)
- Plugging in log(odds)=β0+β1x
17 / 30
by Dr. Lucy D'Agostino McGowan
Transforming odds
- odds = π1−π
- Solving for π
- π=odds1+odds
- Plugging in elog(odds) = odds
- π=elog(odds)1+elog(odds)
- Plugging in log(odds)=β0+β1x
- π=eβ0+β1x1+eβ0+β1x
17 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
- ✌️ forms
| Form | Model |
|---|---|
| Logit form | log(π1−π)=β0+β1x |
| Probability form | π=eβ0+β1x1+eβ0+β1x |
18 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
| probability | odds | log(odds) |
|---|---|---|
| π | π1−π | log(π1−π)=l |
19 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
| probability | odds | log(odds) |
|---|---|---|
| π | π1−π | log(π1−π)=l |
⬅️
| log(odds) | odds | probability |
|---|---|---|
| l | el | el1+el=π |
19 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
- ✌️ forms
20 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
- ✌️ forms
- log(odds): l≈β0+β1x
20 / 30
by Dr. Lucy D'Agostino McGowan
The logistic model
- ✌️ forms
- log(odds): l≈β0+β1x
- P(Outcome = Yes): π≈eβ0+β1x1+eβ0+β1x
20 / 30
by Dr. Lucy D'Agostino McGowan
what are the odds
- Go to RStudio Cloud and open
what are the odds
21 / 30
by Dr. Lucy D'Agostino McGowan
Example
- We are interested in the probability of getting accepted to medical school given a college student's GPA
data("MedGPA")ggplot(MedGPA, aes(Accept, GPA)) + geom_boxplot() + geom_jitter()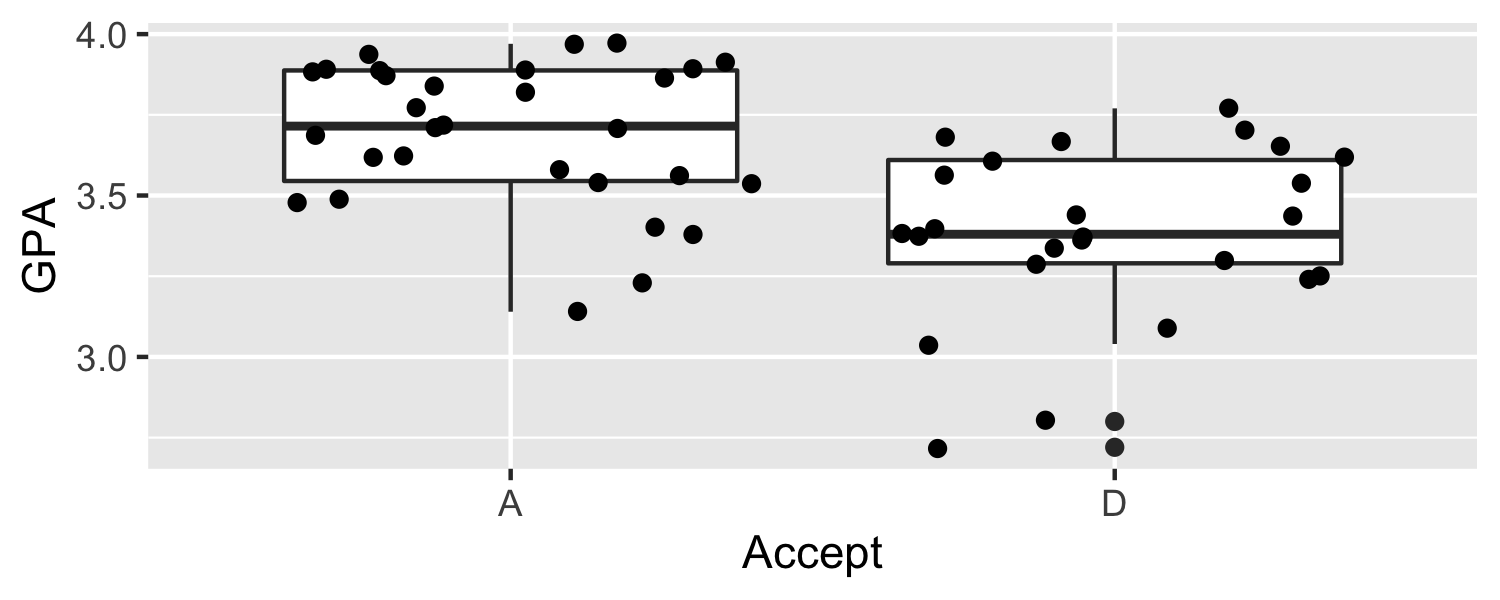
22 / 30
by Dr. Lucy D'Agostino McGowan
Example
What is the equation for the model we are going to fit?
- We are interested in the probability of getting accepted to medical school given a college student's GPA
23 / 30
by Dr. Lucy D'Agostino McGowan
Example
What is the equation for the model we are going to fit?
- log(odds)=β0+β1GPA
- P(Accept) ≈eβ0+β1GPA1+eβ0+β1GPA
- We are interested in the probability of getting accepted to medical school given a college student's GPA
24 / 30
by Dr. Lucy D'Agostino McGowan
Example
- We are interested in the probability of getting accepted to medical school given a college student's GPA
glm(Accept ~ GPA, data = MedGPA, family = "binomial")## ## Call: glm(formula = Accept ~ GPA, family = "binomial", data = MedGPA)## ## Coefficients:## (Intercept) GPA ## 19.21 -5.45 ## ## Degrees of Freedom: 54 Total (i.e. Null); 53 Residual## Null Deviance: 75.8 ## Residual Deviance: 56.8 AIC: 60.825 / 30
by Dr. Lucy D'Agostino McGowan
Example
- We are interested in the probability of getting accepted to medical school given a college student's GPA
glm(Accept ~ GPA, data = MedGPA, family = "binomial") %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 19.2 5.63 3.41 0.000644## 2 GPA -5.45 1.58 -3.45 0.00055326 / 30
by Dr. Lucy D'Agostino McGowan
Example
- We are interested in the probability of getting accepted to medical school given a college student's GPA
glm(Accept ~ GPA, data = MedGPA, family = "binomial") %>% predict()## 1 2 3 4 5 6 7 8 9 10 ## -0.538 -1.737 1.590 -0.919 0.771 -1.083 -2.010 0.990 -1.028 -2.010 ## 11 12 13 14 15 16 17 18 19 20 ## -2.447 0.171 -1.356 -0.483 1.208 -0.101 -0.701 -0.101 1.480 -2.010 ## 21 22 23 24 25 26 27 28 29 30 ## -1.028 -1.356 -2.119 -1.956 -0.865 -0.210 0.444 -0.319 0.662 -1.628 ## 31 32 33 34 35 36 37 38 39 40 ## -0.538 2.353 -2.010 -0.974 1.535 -1.847 -0.101 0.662 -1.901 2.080 ## 41 42 43 44 45 46 47 48 49 50 ## 0.826 0.771 -0.538 -2.283 0.826 0.881 -2.447 2.626 1.262 -0.810 ## 51 52 53 54 55 ## 4.371 -0.210 0.226 3.935 0.44427 / 30
by Dr. Lucy D'Agostino McGowan
Example
- We are interested in the probability of getting accepted to medical school given a college student's GPA
glm(Accept ~ GPA, data = MedGPA, family = "binomial") %>% predict(type = "response")## 1 2 3 4 5 6 7 8 9 10 ## 0.3688 0.1496 0.8306 0.2851 0.6838 0.2529 0.1181 0.7290 0.2634 0.1181 ## 11 12 13 14 15 16 17 18 19 20 ## 0.0797 0.5428 0.2049 0.3815 0.7699 0.4747 0.3315 0.4747 0.8146 0.1181 ## 21 22 23 24 25 26 27 28 29 30 ## 0.2634 0.2049 0.1072 0.1239 0.2963 0.4476 0.6093 0.4208 0.6598 0.1640 ## 31 32 33 34 35 36 37 38 39 40 ## 0.3688 0.9132 0.1181 0.2741 0.8227 0.1363 0.4747 0.6598 0.1300 0.8890 ## 41 42 43 44 45 46 47 48 49 50 ## 0.6955 0.6838 0.3688 0.0925 0.6955 0.7069 0.0797 0.9325 0.7794 0.3078 ## 51 52 53 54 55 ## 0.9875 0.4476 0.5563 0.9808 0.609328 / 30
by Dr. Lucy D'Agostino McGowan
what are the odds
- Go to RStudio Cloud and open
what are the odds - load the
Stat2Data,tidyverse, andbroomlibraries - load
data("MedGPA") - fit the appropriate model predicting
MCATfromGPA - fit the appropriate model predicting
AcceptfromGPA - How do you think you interpret the coefficient for
GPAin the second model?
29 / 30