Variable Transformations Recap

Variable Transformations Recap1 / 19

$\hat{β}$ interpretation in multiple linear regression

The coefficient for $x$ is $\hat{β}$ (95% CI: $L B_{\hat{β}}, U B_{\hat{β}}$ ). A one-unit increase in $x$ yields an expected increase in y of $\hat{β}$ , holding all other variables constant.

2 / 19

${\hat{β}}_{1}$ interpretation in

$s a t = β_{0} + β_{1} s a l a r y + β_{2} (f r a c = L O W) + β_{3} (f r a c = H I G H) + ϵ$

The coefficient for average salary is 1.09 (95% CI: -0.90, 3.08). A one-unit increase in average salary yields an expected increase in average SAT score of 1.09, holding the fraction of students that took the SAT constant.

3 / 19

Adjusting for confoundrs

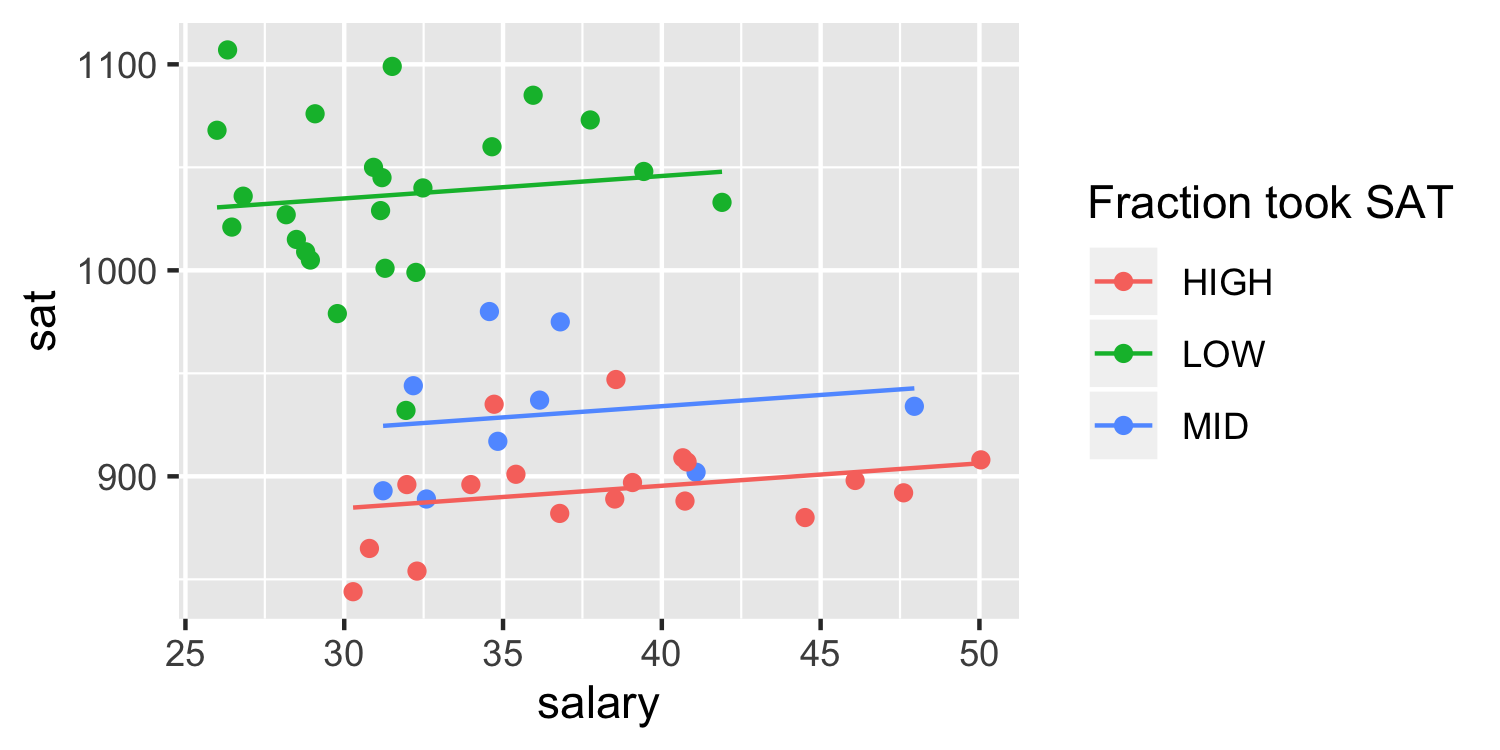
The lines are parallel, the slope ( ${\hat{β}}_{1}$ ) is constant between groups

4 / 19

Interactions

5 / 19

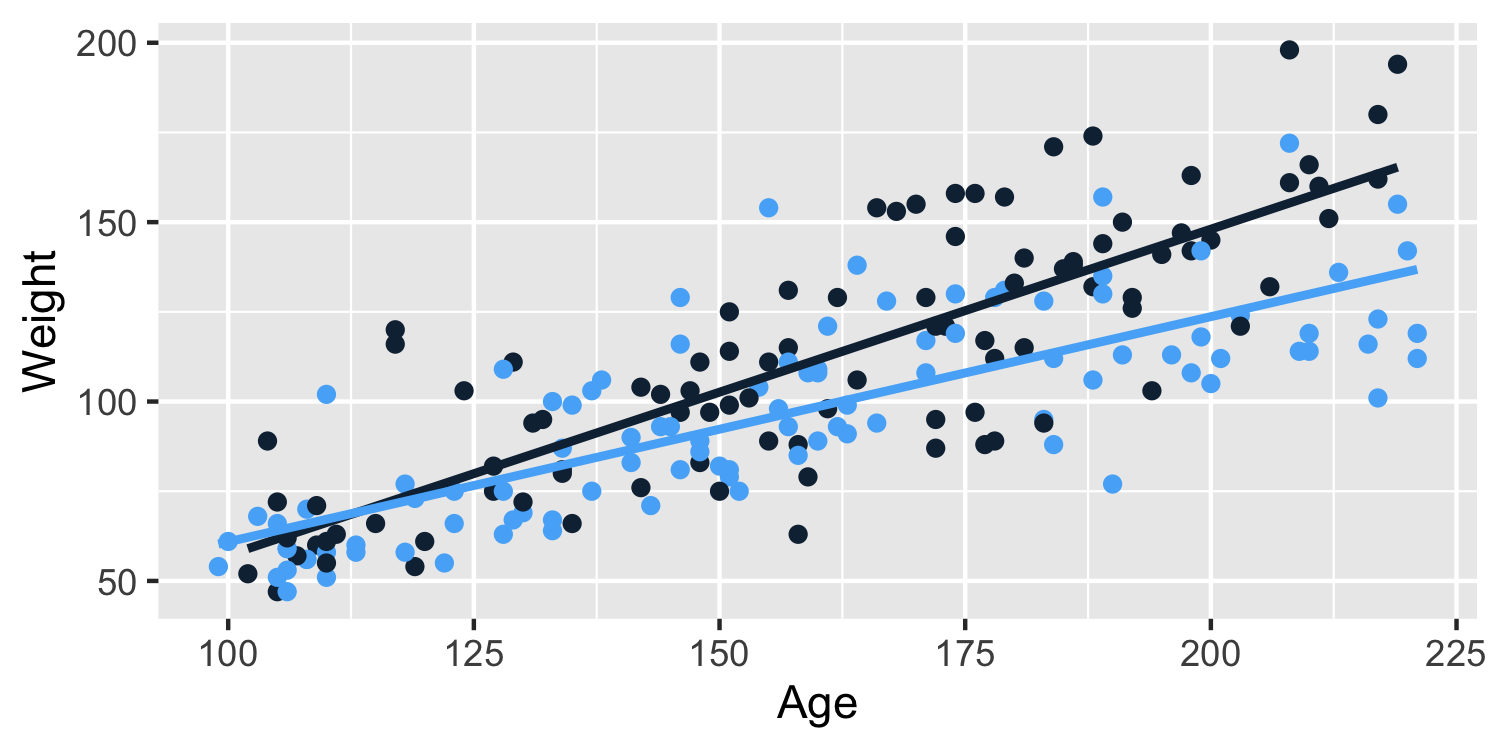
Interactions

😱 the lines cross! That means there is an interaction, that is the slopes differ based on the group

5 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)
- $W e i g h t = β_{0} + β_{1} A g e + ϵ$

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)
- $W e i g h t = β_{0} + β_{1} A g e + ϵ$
What does this model become for girls (When Sex = 1)

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)
- $W e i g h t = β_{0} + β_{1} A g e + ϵ$
What does this model become for girls (When Sex = 1)
- $W e i g h t = β_{0} + β_{1} A g e + β_{2} 1 + β_{3} A g e \times 1 + ϵ$

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)
- $W e i g h t = β_{0} + β_{1} A g e + ϵ$
What does this model become for girls (When Sex = 1)
- $W e i g h t = β_{0} + β_{1} A g e + β_{2} 1 + β_{3} A g e \times 1 + ϵ$
- $W e i g h t = (β_{0} + β_{2}) + (β_{1} + β_{3}) A g e + ϵ$

6 / 19

Interactions

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812

What does this model become for boys (When Sex = 0)
- $W e i g h t = β_{0} + β_{1} A g e + ϵ$
What does this model become for girls (When Sex = 1)
- $W e i g h t = β_{0} + β_{1} A g e + β_{2} 1 + β_{3} A g e \times 1 + ϵ$
- $W e i g h t = (β_{0} + β_{2}) + (β_{1} + β_{3}) A g e + ϵ$
How do you interpret ${\hat{β}}_{0}$ now?

6 / 19

by Dr. Lucy D'Agostino McGowan

Interactionslm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812
What does this model become for boys (When Sex = 0)Weight=β0+β1Age+ϵWeight=β0+β1Age+ϵ

What does this model become for girls (When Sex = 1)Weight=β0+β1Age+β21+β3Age×1+ϵWeight=β0+β1Age+β21+β3Age×1+ϵ
Weight=(β0+β2)+(β1+β3)Age+ϵWeight=(β0+β2)+(β1+β3)Age+ϵ

How do you interpret ^β2β^2 now?
7 / 19

by Dr. Lucy D'Agostino McGowan

Interactionslm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812
What does this model become for boys (When Sex = 0)Weight=β0+β1Age+ϵWeight=β0+β1Age+ϵ

What does this model become for girls (When Sex = 1)Weight=β0+β1Age+β21+β3Age×1+ϵWeight=β0+β1Age+β21+β3Age×1+ϵ
Weight=(β0+β2)+(β1+β3)Age+ϵWeight=(β0+β2)+(β1+β3)Age+ϵ

How do you interpret ^β2β^2 now?The difference in intercepts between boys and girls

7 / 19

by Dr. Lucy D'Agostino McGowan

Interactionslm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812
What does this model become for boys (When Sex = 0)Weight=β0+β1Age+ϵWeight=β0+β1Age+ϵ

What does this model become for girls (When Sex = 1)Weight=β0+β1Age+β21+β3Age×1+ϵWeight=β0+β1Age+β21+β3Age×1+ϵ
Weight=(β0+β2)+(β1+β3)Age+ϵWeight=(β0+β2)+(β1+β3)Age+ϵ

How do you interpret ^β3β^3 now?
8 / 19

by Dr. Lucy D'Agostino McGowan

Interactionslm(Weight ~ Age + Sex + Age * Sex, data = Kids198)

## 
## Call:
## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)
## 
## Coefficients:
## (Intercept)          Age          Sex      Age:Sex  
##    -33.6925       0.9087      31.8506      -0.2812
What does this model become for boys (When Sex = 0)Weight=β0+β1Age+ϵWeight=β0+β1Age+ϵ

What does this model become for girls (When Sex = 1)Weight=β0+β1Age+β21+β3Age×1+ϵWeight=β0+β1Age+β21+β3Age×1+ϵ
Weight=(β0+β2)+(β1+β3)Age+ϵWeight=(β0+β2)+(β1+β3)Age+ϵ

How do you interpret ^β3β^3 now?How much the slope changes as we move from the regression line for boys to that for girls

8 / 19

$\hat{β}$ interpretation for interactions between $x$ and a binary indicator $I$

The coefficient for the interaction between $x$ and $I$ is $\hat{β}$ (95% CI: $L B_{\hat{β}}, U B_{\hat{β}}$ ). This means that the effect of $x$ on $y$ differs by $\hat{β}$ when $I = 1$ compared to $I = 0$ holding all other variables constant*.

9 / 19

$\hat{β}$ interpretation for interactions between $x$ and a binary indicator $I$

You must include this line if there are additional variables in your model.

9 / 19

${\hat{β}}_{3}$ interpretation for

$W e i g h t = β_{0} + β_{1} A g e + β_{2} G i r l + β_{3} A g e \times G i r l + ϵ$

The coefficient for the interaction between Age and Sex is -0.28 (95% CI: -0.44, -0.12). This means that the effect of Age on Weight lower by 0.28 among girls compared to boys.

10 / 19

Non-linear relationships

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds)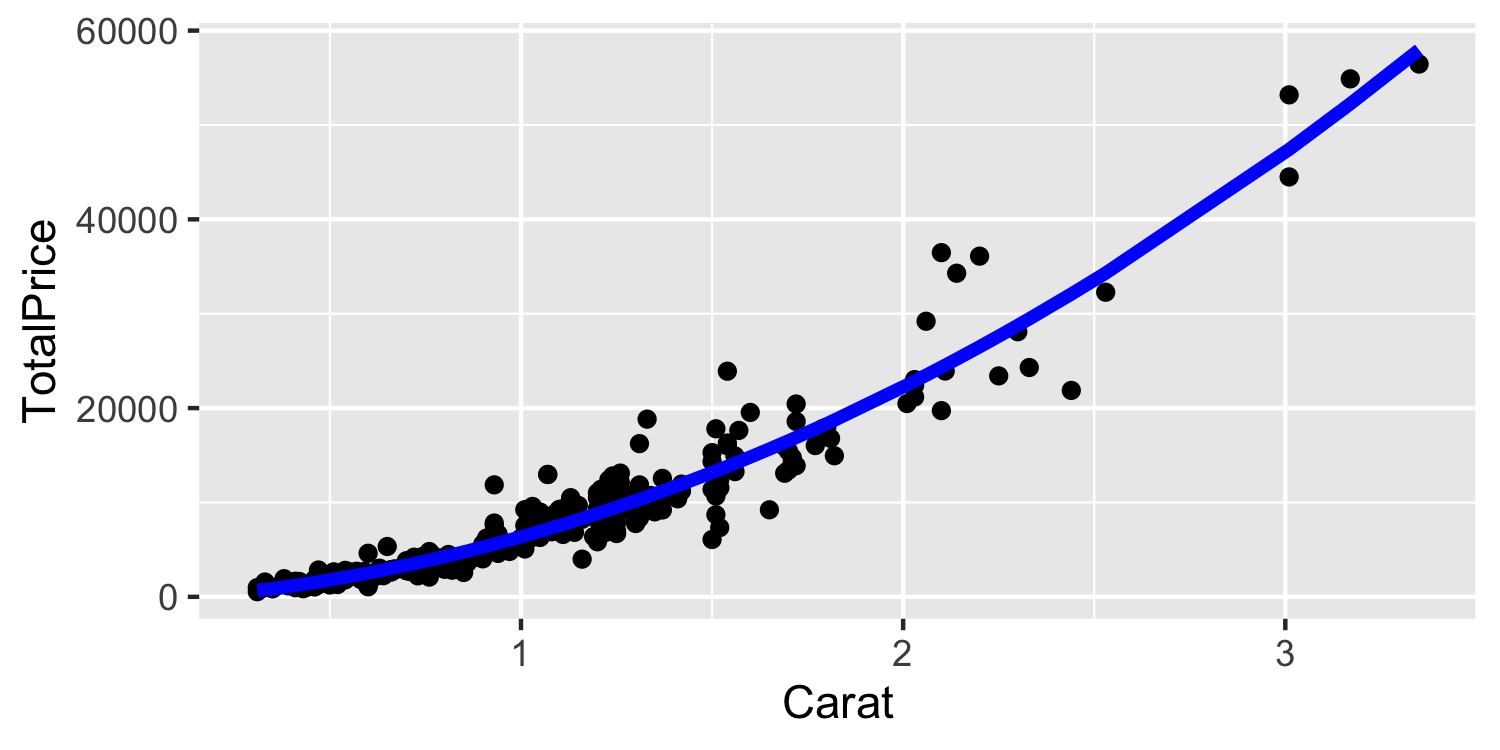

11 / 19

Non-linear relationships

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds)

What is the equation for this relationship?

11 / 19

Interpreting $\hat{β}$ s in the presence of polynomials

$T o t a l P r i c e = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$

What is the interpretation of ${\hat{β}}_{1}$ ?

12 / 19

Interpreting $\hat{β}$ s in the presence of polynomials

$T o t a l P r i c e = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$

What is the interpretation of ${\hat{β}}_{1}$ ?
Typically, in multiple linear regression, the interpretation of ${\hat{β}}_{i}$ is: a one-unit change in $x$ yields an expected change in $y$ of ${\hat{β}}_{i}$ holding all other variables constant.

12 / 19

Interpreting $\hat{β}$ s in the presence of polynomials

$T o t a l P r i c e = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$

What is the interpretation of ${\hat{β}}_{1}$ ?
Typically, in multiple linear regression, the interpretation of ${^β}_{i}$ is: a one-unit change in $x$ yields an expected change in $y$ of ${^β}_{i}$ holding all other variables constant.
- What does it mean to see a change in Caret holding Carat $^{2}$ constant?

12 / 19

Interpreting $\hat{β}$ s in the presence of polynomials

$T o t a l P r i c e = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$

What is the interpretation of ${\hat{β}}_{1}$ ?
Typically, in multiple linear regression, the interpretation of ${^β}_{i}$ is: a one-unit change in $x$ yields an expected change in $y$ of ${^β}_{i}$ holding all other variables constant.
- What does it mean to see a change in Caret holding Carat $^{2}$ constant?
When you have a polynomial term, you need to specify the values you are changing between, since the change is no longer constant across all values of $x$ .

12 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?

13 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?

(-522.7 + 2386 * 1.8 + 4498.2 * 1.8^2) - 
  (-522.7 + 2386 * 0.8 + 4498.2 * 0.8^2)

## [1] 14081.32

13 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?

(-522.7 + 2386 * 1.8 + 4498.2 * 1.8^2) - 
  (-522.7 + 2386 * 0.8 + 4498.2 * 0.8^2)

## [1] 14081.32

2386 * (1.8 - 0.8) + 
  4498.2 * (1.8^2 - 0.8^2)

## [1] 14081.32

13 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?

14 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?

2386 * (2.8 - 1.8) + 4498.2 * (2.8^2 - 1.8^2)

## [1] 23077.72

14 / 19

Interpreting $\hat{β}$ in the presence of polynomials

lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>%
  tidy()

## # A tibble: 3 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    -523.      466.     -1.12 2.63e- 1
## 2 Carat          2386.      753.      3.17 1.66e- 3
## 3 I(Carat^2)     4498.      263.     17.1  5.09e-48

What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?

2386  (2.8 - 1.8) + 4498.2  (2.8^2 - 1.8^2)

## [1] 23077.72

Can we talk about ${\hat{β}}_{1}$ and ${\hat{β}}_{2}$ in the context of a one-unit change in Carat?

14 / 19

by Dr. Lucy D'Agostino McGowan

Interpreting ^ββ^ in the presence of polynomials^ββ^ coefficients that are transformations of the same xx variable must be interpreted together
15 / 19

by Dr. Lucy D'Agostino McGowan

Interpreting ^ββ^ in the presence of polynomials^ββ^ coefficients that are transformations of the same xx variable must be interpreted together
You must first choose to values of xx to change between, and then report the change. 
15 / 19

by Dr. Lucy D'Agostino McGowan

Interpreting ^ββ^ in the presence of polynomials^ββ^ coefficients that are transformations of the same xx variable must be interpreted together
You must first choose to values of xx to change between, and then report the change. 
A sensible choice for the two xx values can be the 25th% quantile and the 75th% quantile.
15 / 19

General $\hat{β}$ interpretation with quadratic terms

The linear term in the model for $x$ has a coefficient of ${\hat{β}}_{1}$ (95% CI: $(L B_{{\hat{β}}_{1}}, U B_{{\hat{β}}_{1}})$ ). The quadratic term in the model for $x$ has a coefficient of ${\hat{β}}_{2}$ (95% CI: $(L B_{{\hat{β}}_{2}}, U B_{{\hat{β}}_{2}})$ ). A change in $x$ from $a$ to $b$ yields an expected change in $y$ of ${\hat{β}}_{1} (b - a) + {\hat{β}}_{2} (b^{2} - a^{2})$ holding all other variables constant*.

16 / 19

General $\hat{β}$ interpretation with quadratic terms

You must include this line if there are additional variables in your model.

16 / 19

Specific $\hat{β}$ interpretation for $y = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$ model

The linear term in the model for Carat has a coefficient of 2386 (95% CI: $(906, 3866)$ ). The quadratic term in the model for Carat has a coefficient of $4498$ (95% CI: $(3981, 5016)$ ). A change in Carat from $0.7$ to $1.24$ yields an expected change in TotalPrice of $6000.5$ .

17 / 19

Specific $\hat{β}$ interpretation for $y = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$ model

Where did I get 0.7 and 1.24?

17 / 19

Quantiles

Diamonds %>%
  summarise(q1 = quantile(Carat, 0.25),
            q3 = quantile(Carat, 0.75))

##    q1   q3
## 1 0.7 1.24

18 / 19

by Dr. Lucy D'Agostino McGowan

 DiamondsGo to RStudio Cloud and open Diamonds
Fit the model  TotalPrice=β0+β1Carat+β2Carat2+β3Color+ϵTotalPrice=β0+β1Carat+β2Carat2+β3Color+ϵ
Find the 0.25 quantile and 0.75 quantile of Carat
What is the interpretation of ^β1β^1, ^β2β^2, and ^β3β^3?
19 / 19

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Variable Transformations Recap

^ββ^ interpretation in multiple linear regression

^β1β^1 interpretation in

Adjusting for confoundrs

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

Interactions

^ββ^ interpretation for interactions between xx and a binary indicator II

^ββ^ interpretation for interactions between xx and a binary indicator II

^β3β^3 interpretation for

Non-linear relationships

Non-linear relationships

Interpreting ^ββ^s in the presence of polynomials

Interpreting ^ββ^s in the presence of polynomials

Interpreting ^ββ^s in the presence of polynomials

Interpreting ^ββ^s in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

Interpreting ^ββ^ in the presence of polynomials

General ^ββ^ interpretation with quadratic terms

General ^ββ^ interpretation with quadratic terms

Specific ^ββ^ interpretation for y=β0+β1Carat+β2Carat2+ϵy=β0+β1Carat+β2Carat2+ϵ model

Specific ^ββ^ interpretation for y=β0+β1Carat+β2Carat2+ϵy=β0+β1Carat+β2Carat2+ϵ model

Quantiles

Diamonds

^ββ^ interpretation in multiple linear regression

Help

$\hat{β}$ interpretation in multiple linear regression

${\hat{β}}_{1}$ interpretation in

$\hat{β}$ interpretation for interactions between $x$ and a binary indicator $I$

$\hat{β}$ interpretation for interactions between $x$ and a binary indicator $I$

${\hat{β}}_{3}$ interpretation for

Interpreting $\hat{β}$ s in the presence of polynomials

Interpreting $\hat{β}$ s in the presence of polynomials

Interpreting $\hat{β}$ s in the presence of polynomials

Interpreting $\hat{β}$ s in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

Interpreting $\hat{β}$ in the presence of polynomials

General $\hat{β}$ interpretation with quadratic terms

General $\hat{β}$ interpretation with quadratic terms

Specific $\hat{β}$ interpretation for $y = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$ model

Specific $\hat{β}$ interpretation for $y = β_{0} + β_{1} C a r a t + β_{2} C a r a t^{2} + ϵ$ model

`Diamonds`

$\hat{β}$ interpretation in multiple linear regression