Confounding and Variable Transformations
Adjusting for confounders
- What is the relationship between average SAT scores and average teacher salaries?
Adjusting for confounders
- What is the relationship between average SAT scores and average teacher salaries?
- Are we doing inference or prediction?
Adjusting for confounders
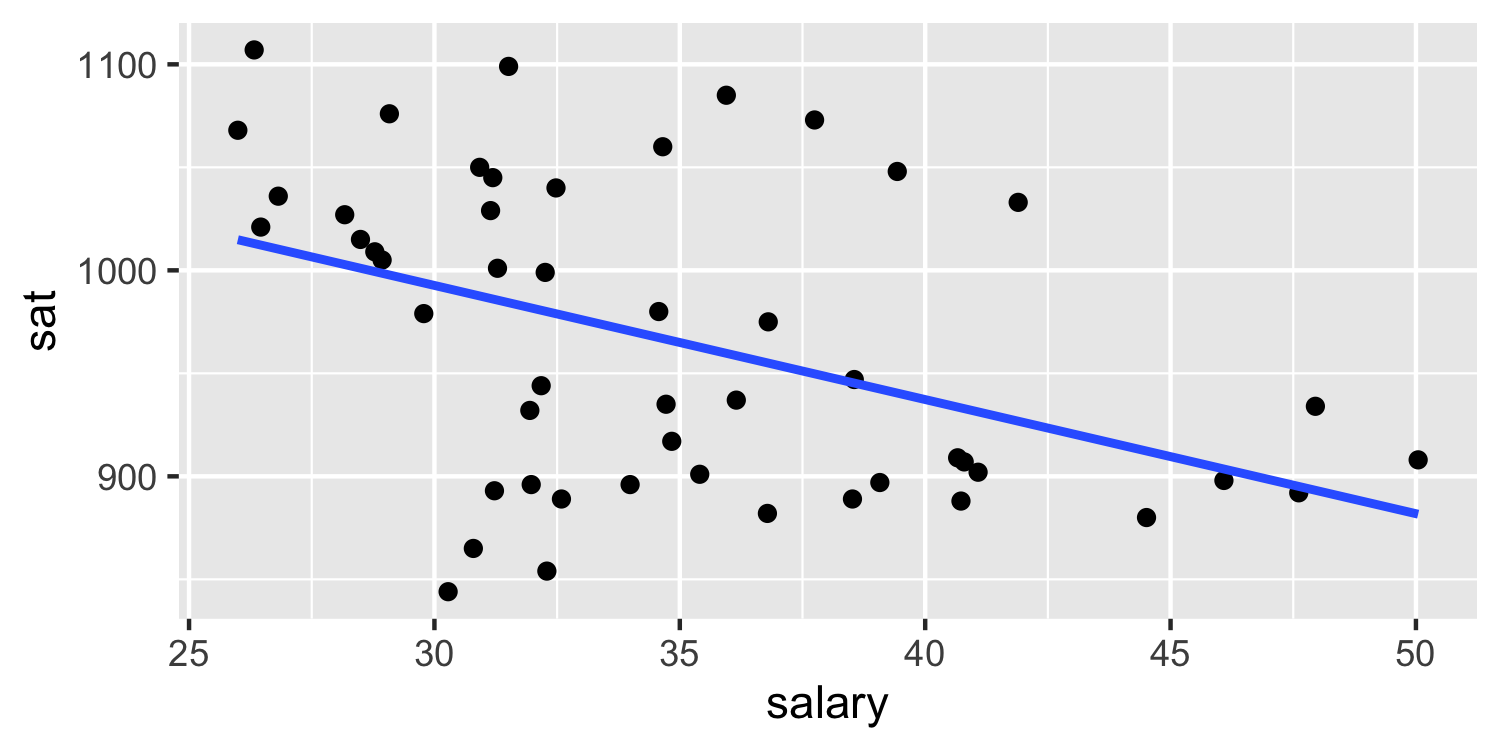
- I fit a linear model for ^sat=^β0+^β1salary
## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1159. 57.7 20.1 5.13e-25## 2 salary -5.54 1.63 -3.39 1.39e- 3Adjusting for confounders
- I fit a linear model for ^sat=^β0+^β1salary
## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1159. 57.7 20.1 5.13e-25## 2 salary -5.54 1.63 -3.39 1.39e- 3- How do we interpret this result?
Adjusting for confounders
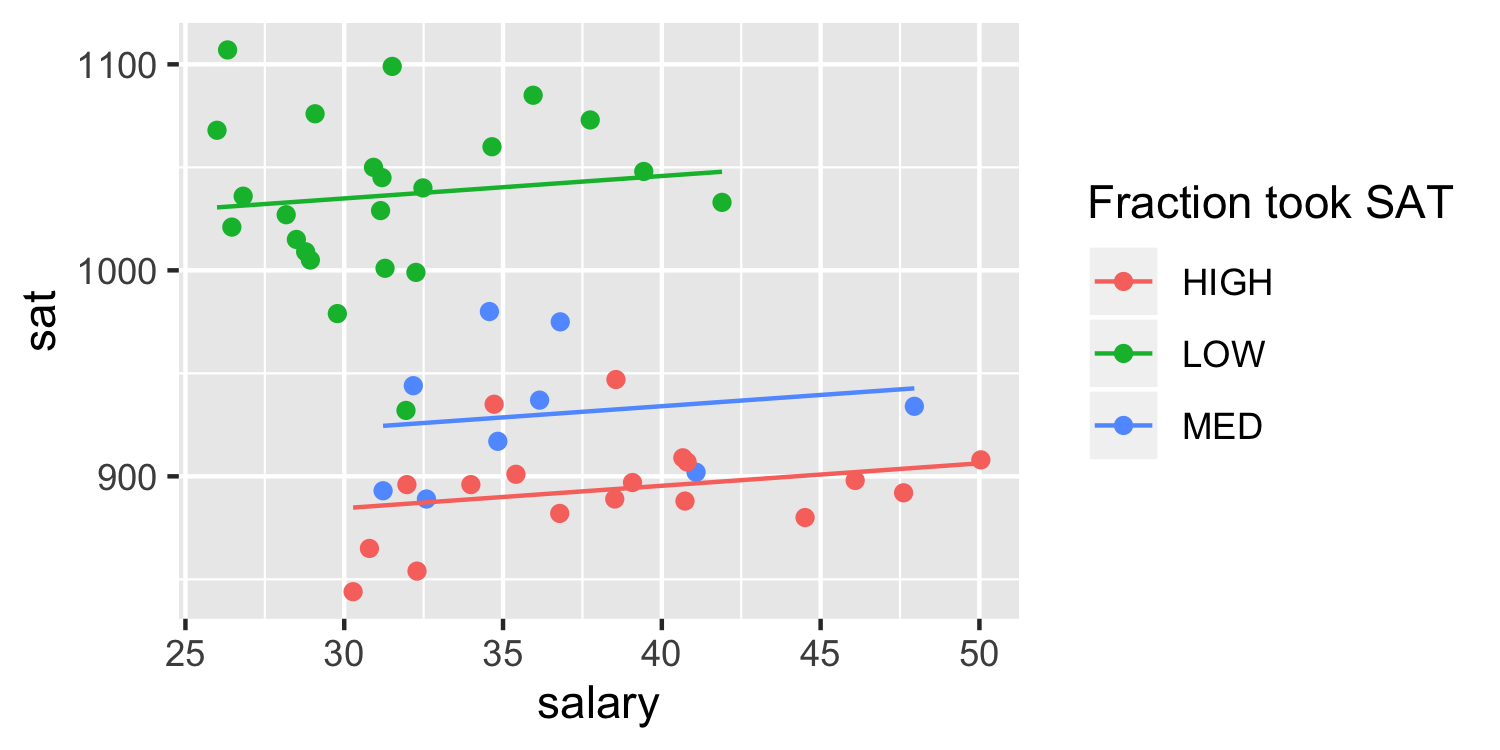
- There is a third variable, the fraction of students that took the SAT in that state. It is grouped as "Low", "Medium", and, "High".
## # A tibble: 4 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 852. 38.9 21.9 5.56e-26## 2 salary 1.09 0.988 1.10 2.76e- 1## 3 frac_groupLOW 150. 12.8 11.7 2.09e-15## 4 frac_groupMED 38.6 14.1 2.75 8.59e- 3Adjusting for confounders
- There is a third variable, the fraction of students that took the SAT in that state. It is grouped as "Low", "Medium", and, "High".
## # A tibble: 4 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 852. 38.9 21.9 5.56e-26## 2 salary 1.09 0.988 1.10 2.76e- 1## 3 frac_groupLOW 150. 12.8 11.7 2.09e-15## 4 frac_groupMED 38.6 14.1 2.75 8.59e- 3- What is the referent category?
Adjusting for confounders
- There is a third variable, the fraction of students that took the SAT in that state. It is grouped as "Low", "Medium", and, "High".
## # A tibble: 4 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 852. 38.9 21.9 5.56e-26## 2 salary 1.09 0.988 1.10 2.76e- 1## 3 frac_groupLOW 150. 12.8 11.7 2.09e-15## 4 frac_groupMED 38.6 14.1 2.75 8.59e- 3- What is the referent category?
- How do you interpret the ^β for
frac_groupLOW?
Adjusting for confounders
- There is a third variable, the fraction of students that took the SAT in that state. It is grouped as "Low", "Medium", and, "High".
## # A tibble: 4 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 852. 38.9 21.9 5.56e-26## 2 salary 1.09 0.988 1.10 2.76e- 1## 3 frac_groupLOW 150. 12.8 11.7 2.09e-15## 4 frac_groupMED 38.6 14.1 2.75 8.59e- 3- What is the referent category?
- How do you interpret the ^β for
frac_groupLOW? - How do you interpret the ^β for
salarynow?
^β interpretation in multiple linear regression
The coefficient for x is ^β (95% CI: LB^β,UB^β). A one-unit increase in x yields an expected increase in y of ^β, holding all other variables constant.
^β interpretation in multiple linear regression
The coefficient for average salary is 1.09 (95% CI: -0.90, 3.08). A one-unit increase in average salary yields an expected increase in average SAT score of 1.09, holding the fraction of students that took the SAT constant.
Adjusting for confounders
Adjusting for confoundrs
Adjusting for confoundrs

- What is this called? Where the direction reverses?
Adjusting for confoundrs

- What is this called? Where the direction reverses?
- Notice here the lines are parallel so holding the group constant, this is the effect we see.
Adjusting for confoundrs

- What is this called? Where the direction reverses?
- Notice here the lines are parallel so holding the group constant, this is the effect we see.
- 😱 what if the lines aren't parallel?
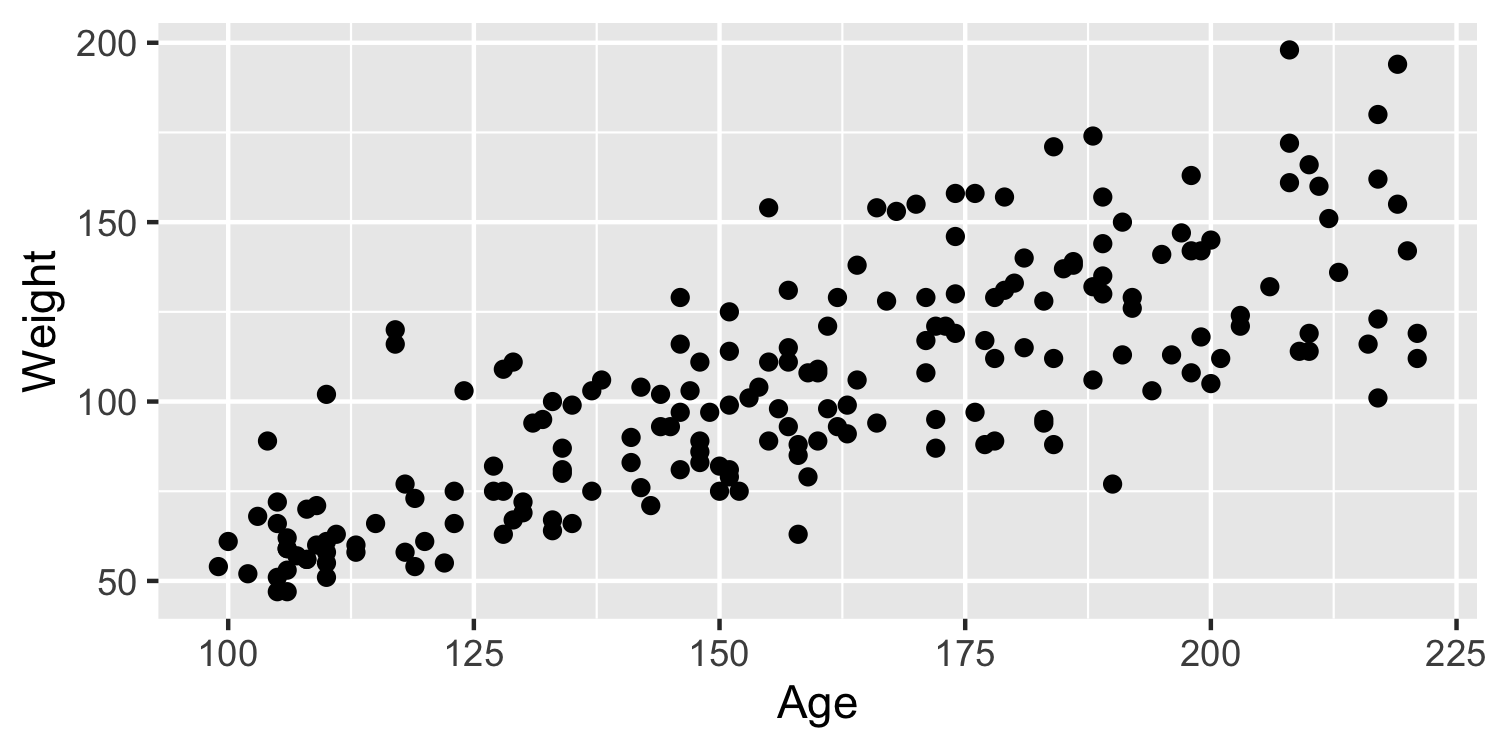
Interactions
Interactions

- Will ^βage be positive or negative?
Interactions
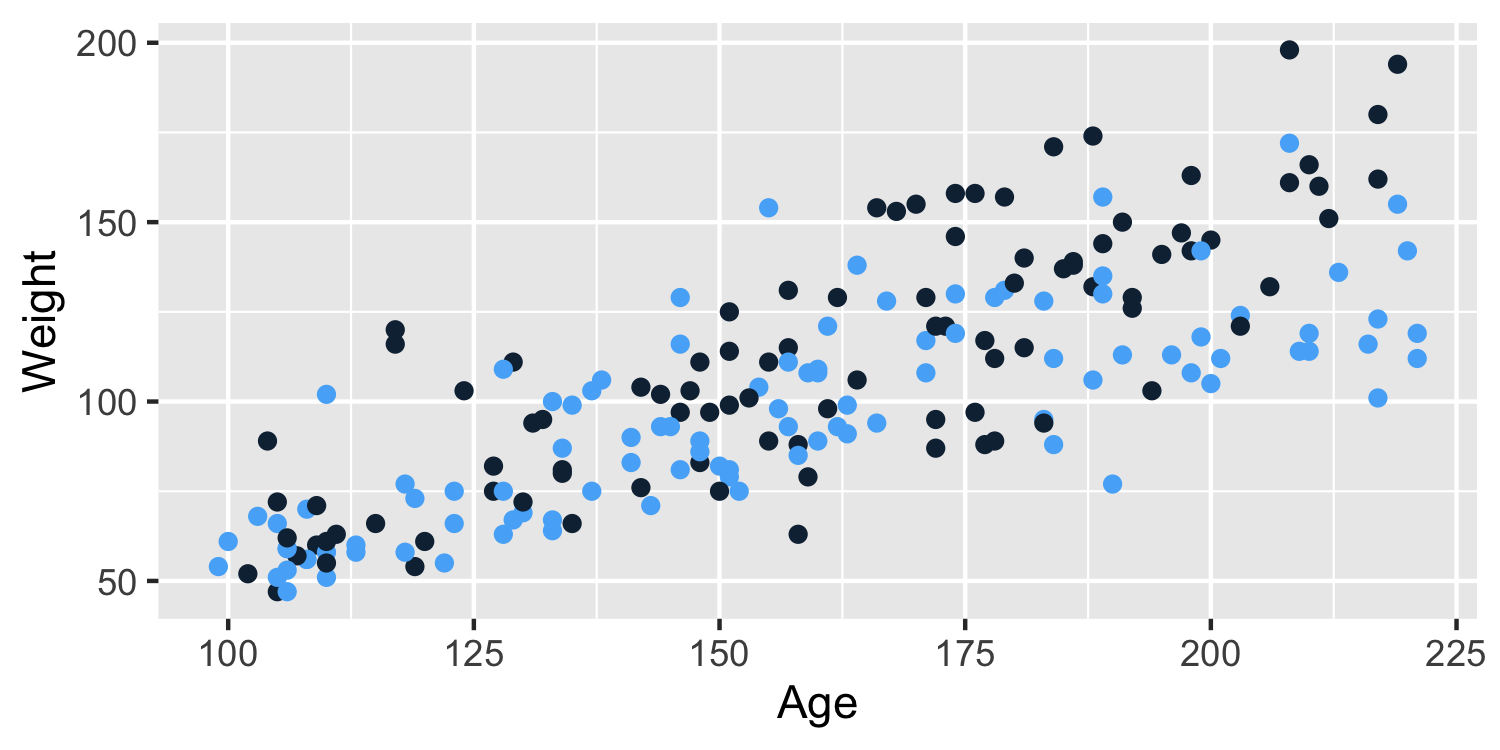
- Let's look at this relationship split by
sex(blue: Girl, black: Boy)
Interactions
- Let's look at this relationship split by
sex(blue: Girl, black: Boy)
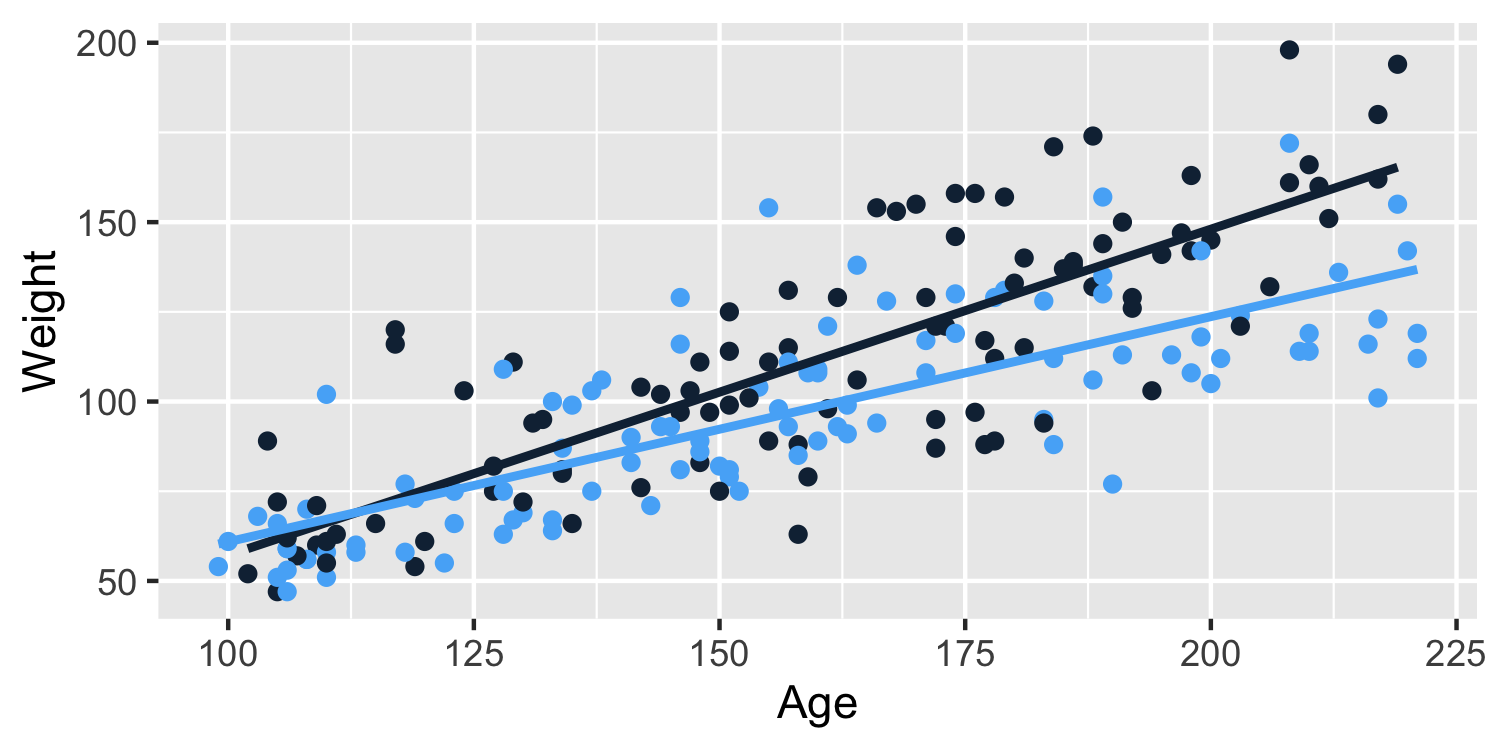
Interactions
- Let's look at this relationship split by
sex(blue: Girl, black: Boy)

- 😱 the lines cross! That means there is an interaction, that is the slopes differ based on the group
Interactions
- Let's look at this relationship split by
sex(blue: Girl, black: Boy)
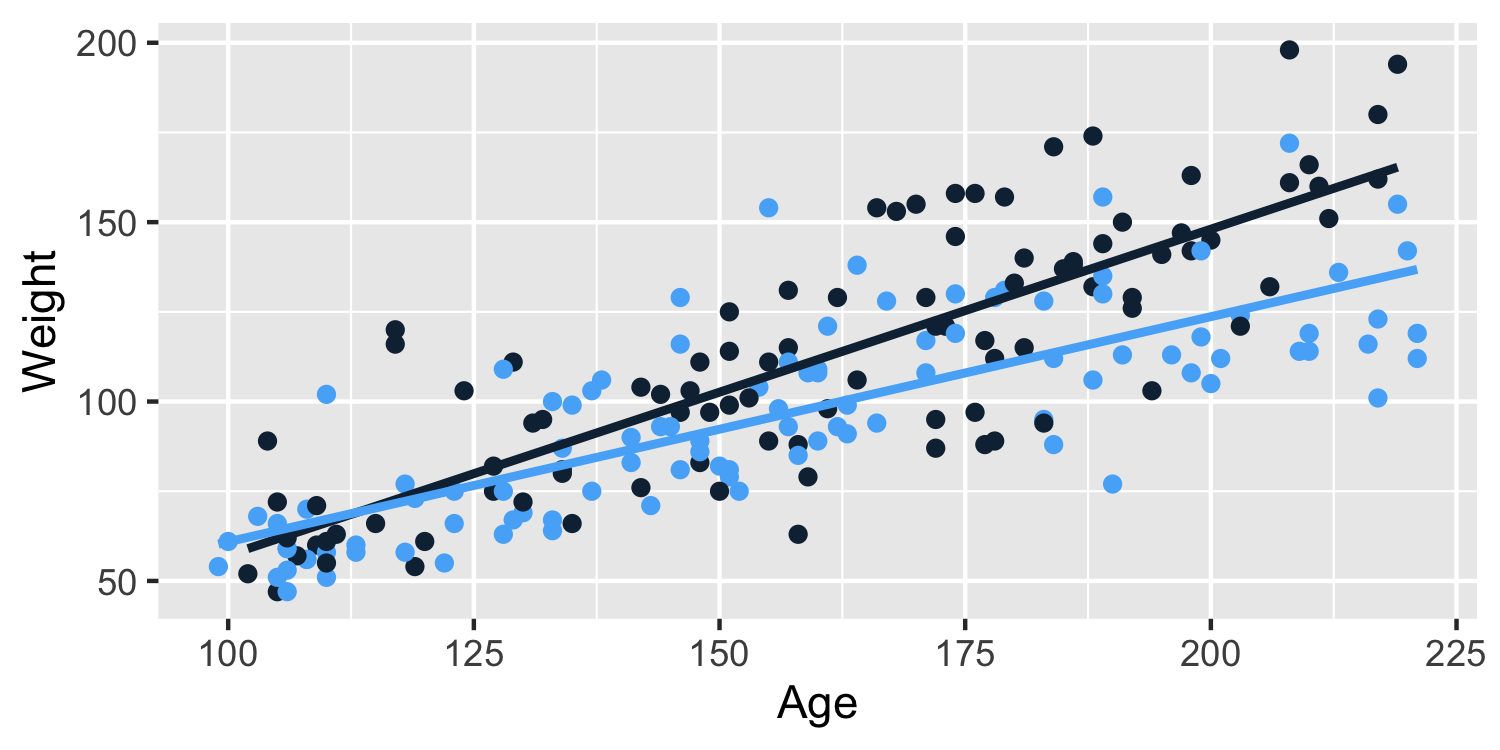
Interactions
- Let's look at this relationship split by
sex(blue: Girl, black: Boy)

- What is the equation for this relationship?
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
- How do you interpret ^β0 now?
Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
- How do you interpret ^β2 now?
Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
- How do you interpret ^β2 now?
- The difference in intercepts between boys and girls
Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
- How do you interpret ^β3 now?
Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Call:## lm(formula = Weight ~ Age + Sex + Age * Sex, data = Kids198)## ## Coefficients:## (Intercept) Age Sex Age:Sex ## -33.6925 0.9087 31.8506 -0.2812- What does this model become for boys (When
Sex = 0)- Weight=β0+β1Age+ϵ
- What does this model become for girls (When
Sex = 1)- Weight=β0+β1Age+β21+β3Age×1+ϵ
- Weight=(β0+β2)+(β1+β3)Age+ϵ
- How do you interpret ^β3 now?
- How much the slope changes as we move from the regression line for boys to that for girls
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
- Hypothesis testing: What if you want to test whether the slope is different between groups?
- Is the growth rate different for boys and girls?
- What is H0?
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
- Hypothesis testing: What if you want to test whether the slope is different between groups?
- Is the growth rate different for boys and girls?
- What is H0?
- H0:β3=0
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
- Hypothesis testing: What if you want to test whether the slope is different between groups?
- Is the growth rate different for boys and girls?
- What is H0?
- H0:β3=0
- What is HA?
Interactions
Weight=β0+β1Age+β2Girl+β3Age×Girl+ϵ
- Hypothesis testing: What if you want to test whether the slope is different between groups?
- Is the growth rate different for boys and girls?
- What is H0?
- H0:β3=0
- What is HA?
- HA:β3≠0
Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198) %>% tidy(conf.int = TRUE)## # A tibble: 4 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -33.7 10.0 -3.37 9.17e- 4 -53.4 -14.0 ## 2 Age 0.909 0.0611 14.9 6.47e-34 0.788 1.03 ## 3 Sex 31.9 13.2 2.41 1.71e- 2 5.73 58.0 ## 4 Age:Sex -0.281 0.0816 -3.44 7.00e- 4 -0.442 -0.120Interactions
lm(Weight ~ Age + Sex + Age * Sex, data = Kids198) %>% tidy(conf.int = TRUE)## # A tibble: 4 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -33.7 10.0 -3.37 9.17e- 4 -53.4 -14.0 ## 2 Age 0.909 0.0611 14.9 6.47e-34 0.788 1.03 ## 3 Sex 31.9 13.2 2.41 1.71e- 2 5.73 58.0 ## 4 Age:Sex -0.281 0.0816 -3.44 7.00e- 4 -0.442 -0.120- What is the result of our hypothesis test?
^β interpretation for interactions between x and a binary indicator I
The coefficient for the interaction between x and I is ^β (95% CI: LB^β,UB^β). This means that the effect of x on y differs by ^β when I=1 compared to I=0 holding all other variables constant*.
^β interpretation for interactions between x and a binary indicator I
The coefficient for the interaction between x and I is ^β (95% CI: LB^β,UB^β). This means that the effect of x on y differs by ^β when I=1 compared to I=0 holding all other variables constant*.
- You must include this line if there are additional variables in your model.
^β interpretation for interactions between x and a binary indicator I
The coefficient for the interaction between Age and Sex is -0.28 (95% CI: -0.44, -0.12). This means that the effect of Age on Weight lower by 0.28 among girls compared to boys.
Non-linear relationships
- Sometimes the relationships between the outcome y and x variables are nonlinear.
- We can use polynomials to address this!
- Returning to the Diamonds data, let's say we are interested in predicting Total Price from the Carats.
Non-linear relationships
- Sometimes the relationships between the outcome y and x variables are nonlinear.
- We can use polynomials to address this!
- Returning to the Diamonds data, let's say we are interested in predicting Total Price from the Carats.
- Is this an example of inference or prediction?
Non-linear relationships
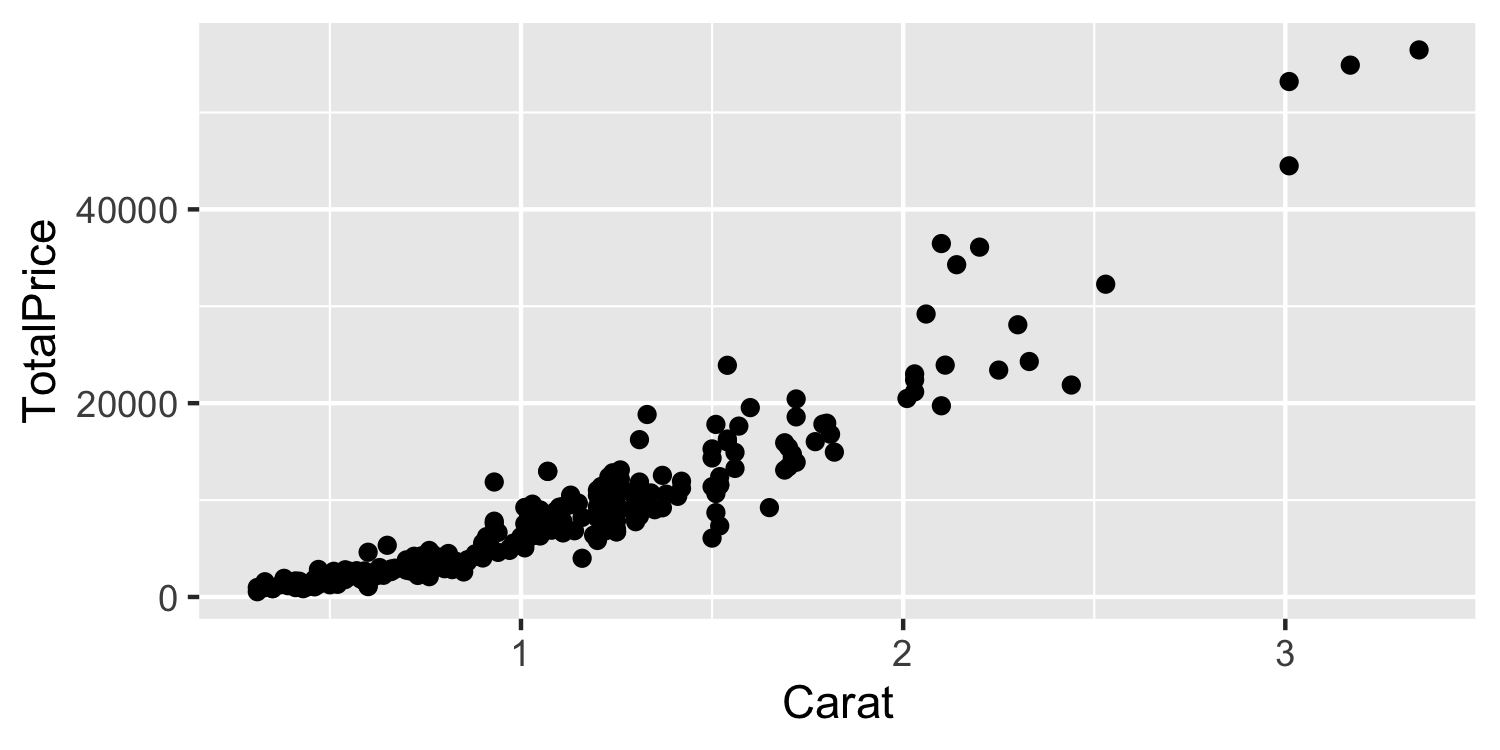
Non-linear relationships
lm(TotalPrice ~ Carat, data = Diamonds)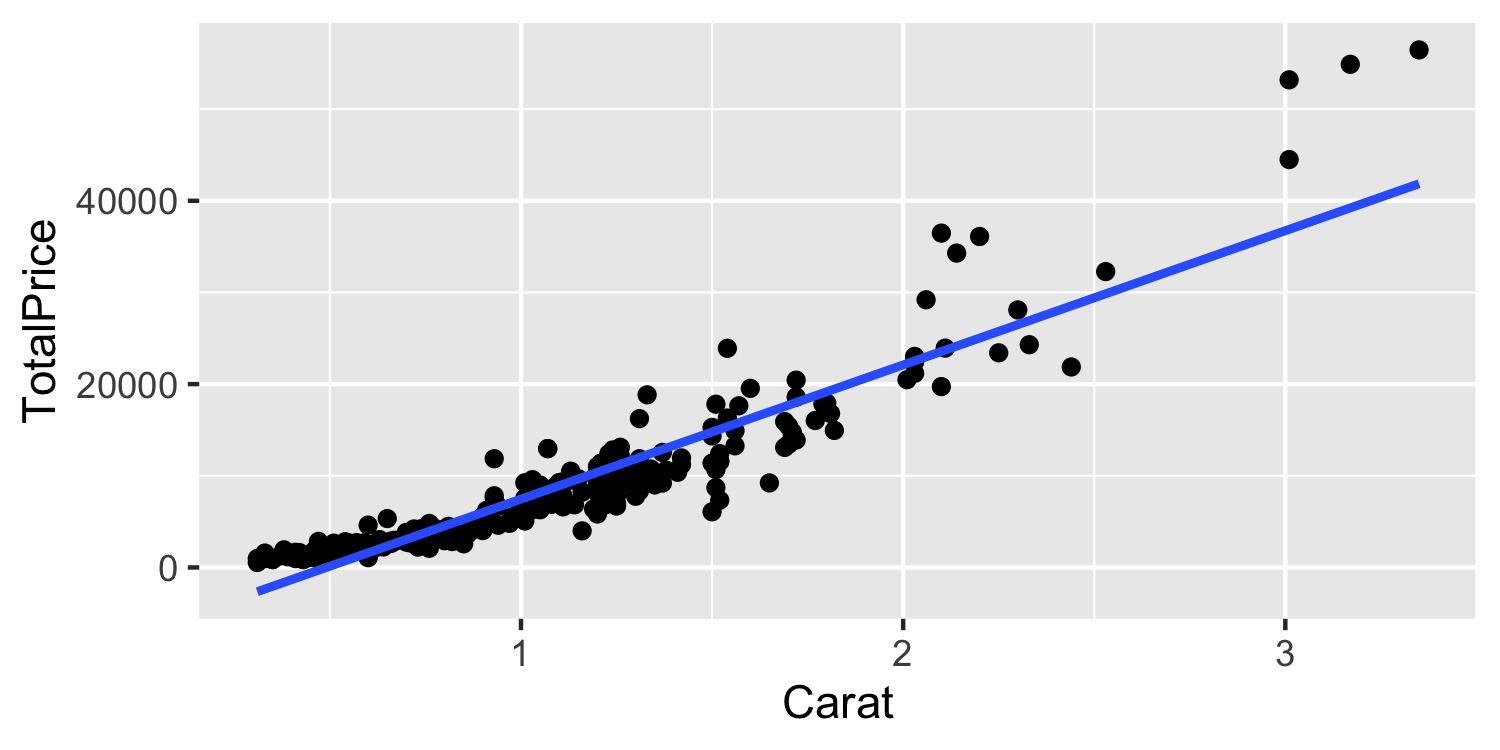
Non-linear relationships
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds)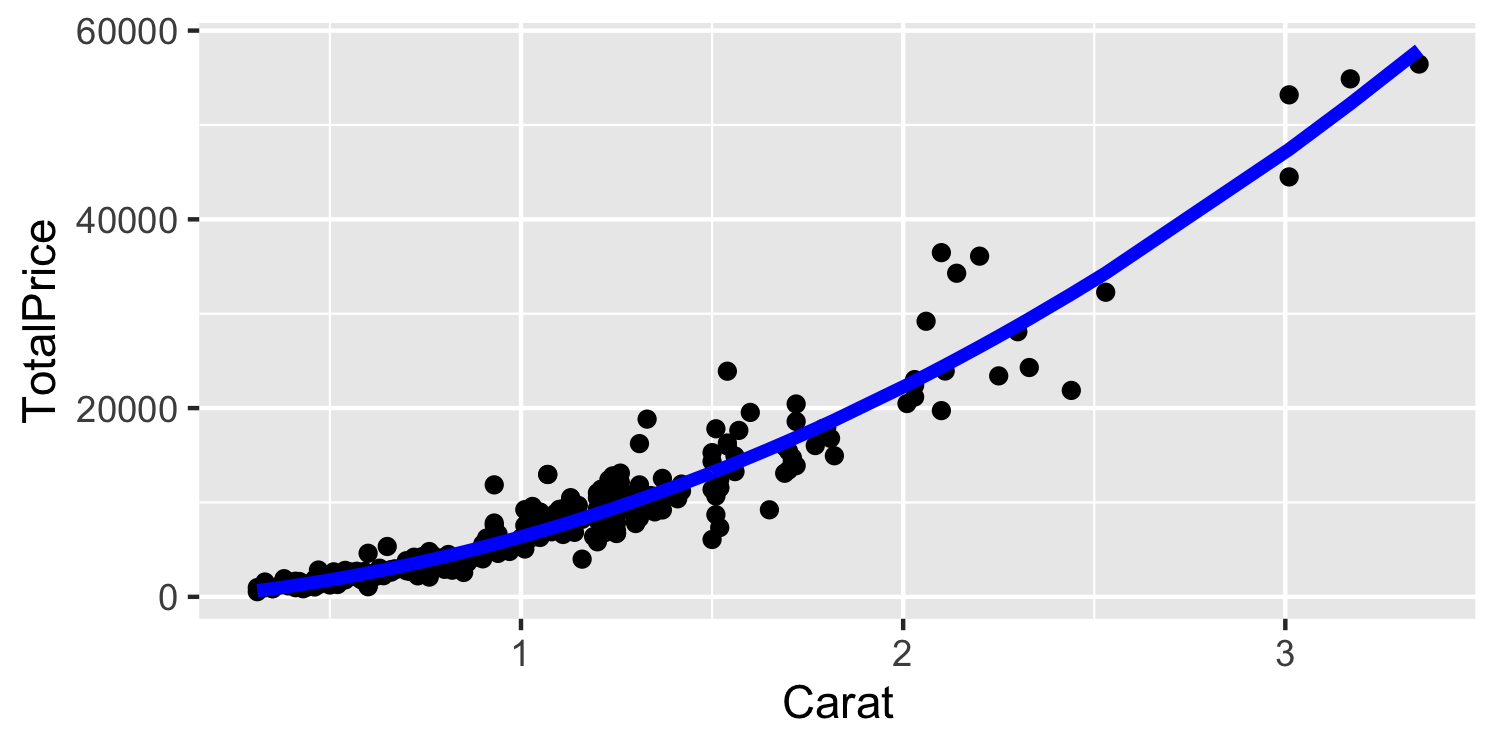
Non-linear relationships
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds)
- What is the equation for this relationship?
Interpreting ^βs in the presence of polynomials
TotalPrice=β0+β1Carat+β2Carat2+ϵ
- What is the interpretation of ^β1?
Interpreting ^βs in the presence of polynomials
TotalPrice=β0+β1Carat+β2Carat2+ϵ
- What is the interpretation of ^β1?
- Typically, in multiple linear regression, the interpretation of ^βi is: a one-unit change in x yields an expected change in y of ^βi holding all other variables constant.
Interpreting ^βs in the presence of polynomials
TotalPrice=β0+β1Carat+β2Carat2+ϵ
- What is the interpretation of ^β1?
- Typically, in multiple linear regression, the interpretation of ^βi is:
a one-unit change in x yields an expected change in y of ^βi holding all other variables constant.
- What does it mean to see a change in
CaretholdingCarat2 constant?
- What does it mean to see a change in
Interpreting ^βs in the presence of polynomials
TotalPrice=β0+β1Carat+β2Carat2+ϵ
- What is the interpretation of ^β1?
- Typically, in multiple linear regression, the interpretation of ^βi is:
a one-unit change in x yields an expected change in y of ^βi holding all other variables constant.
- What does it mean to see a change in
CaretholdingCarat2 constant?
- What does it mean to see a change in
- When you have a polynomial term, you need to specify the values you are changing between, since the change is no longer constant across all values of x.
Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?
Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?
(-522.7 + 2386 * 1.8 + 4498.2 * 1.8^2) - (-522.7 + 2386 * 0.8 + 4498.2 * 0.8^2)## [1] 14081.32Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 0.8 to 1.8?
(-522.7 + 2386 * 1.8 + 4498.2 * 1.8^2) - (-522.7 + 2386 * 0.8 + 4498.2 * 0.8^2)## [1] 14081.322386 * (1.8 - 0.8) + 4498.2 * (1.8^2 - 0.8^2)## [1] 14081.32Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?
Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?
2386 * (2.8 - 1.8) + 4498.2 * (2.8^2 - 1.8^2)## [1] 23077.72Interpreting ^β in the presence of polynomials
lm(TotalPrice ~ Carat + I(Carat^2), data = Diamonds) %>% tidy()## # A tibble: 3 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) -523. 466. -1.12 2.63e- 1## 2 Carat 2386. 753. 3.17 1.66e- 3## 3 I(Carat^2) 4498. 263. 17.1 5.09e-48What is the expected change in TotalPrice for a one-unit change in Carat, changing from 1.8 to 2.8?
2386 (2.8 - 1.8) + 4498.2 (2.8^2 - 1.8^2)## [1] 23077.72- Can we talk about ^β1 and ^β2 in the context of a one-unit change in
Carat?
Interpreting ^β in the presence of polynomials
- ^β coefficients that are transformations of the same x variable must be interpreted together
Interpreting ^β in the presence of polynomials
- ^β coefficients that are transformations of the same x variable must be interpreted together
- You must first choose to values of x to change between, and then report the change.
Interpreting ^β in the presence of polynomials
- ^β coefficients that are transformations of the same x variable must be interpreted together
- You must first choose to values of x to change between, and then report the change.
- A sensible choice for the two x values can be the 25th% quantile and the 75th% quantile.
General ^β interpretation with quadratic terms
The linear term in the model for x has a coefficient of ^β1 (95% CI: (LB^β1,UB^β1)). The quadratic term in the model for x has a coefficient of ^β2 (95% CI: (LB^β2,UB^β2)). A change in x from a to b yields an expected change in y of ^β1(b−a)+^β2(b2−a2) holding all other variables constant*.
General ^β interpretation with quadratic terms
The linear term in the model for x has a coefficient of ^β1 (95% CI: (LB^β1,UB^β1)). The quadratic term in the model for x has a coefficient of ^β2 (95% CI: (LB^β2,UB^β2)). A change in x from a to b yields an expected change in y of ^β1(b−a)+^β2(b2−a2) holding all other variables constant*.
- You must include this line if there are additional variables in your model.
Specific ^β interpretation for y=β0+β1Carat+β2Carat2+ϵ model
The linear term in the model for Carat has a coefficient of 2386 (95% CI: (906,3866)). The quadratic term in the model for Carat has a coefficient of 4498 (95% CI: (3981,5016)). A change in Carat from 0.7 to 1.24 yields an expected change in TotalPrice of 6000.5.
Specific ^β interpretation for y=β0+β1Carat+β2Carat2+ϵ model
The linear term in the model for Carat has a coefficient of 2386 (95% CI: (906,3866)). The quadratic term in the model for Carat has a coefficient of 4498 (95% CI: (3981,5016)). A change in Carat from 0.7 to 1.24 yields an expected change in TotalPrice of 6000.5.
- Why didn't I say holding all other variables constant?
Take aways
- The interpretation of ^β in multiple linear regression
- A one-unit change in x yields an expected change in y of ^β holding all other included variables constant
Take aways
- The interpretation of ^β in multiple linear regression
- A one-unit change in x yields an expected change in y of ^β holding all other included variables constant
- If the slope differs between groups (the lines cross in a scatterplot), an interaction is present
Take aways
- The interpretation of ^β in multiple linear regression
- A one-unit change in x yields an expected change in y of ^β holding all other included variables constant
- If the slope differs between groups (the lines cross in a scatterplot), an interaction is present
- You can include polynomial terms to address non-linear relationships
Take aways
- The interpretation of ^β in multiple linear regression
- A one-unit change in x yields an expected change in y of ^β holding all other included variables constant
- If the slope differs between groups (the lines cross in a scatterplot), an interaction is present
- You can include polynomial terms to address non-linear relationships
- The coefficients for a polynomial must be interpreted together
Diamonds
- Go to RStudio Cloud and open
Diamonds - Fit the model TotalPrice=β0+β1Carat+β2Carat2+β3Color+ϵ
- Find the 0.25 quantile and 0.75 quantile of
Carat - What is the interpretation of ^β1, ^β2, and ^β3?