class: center, middle, inverse, title-slide # Partitioning variability --- layout: true <div class="my-footer"> <span> by Dr. Lucy D'Agostino McGowan </span> </div> --- # Partitioning variability  --- # Why? * `\(\Huge y − \bar{y} = (\hat{y} − \bar{y}) + (y − \hat{y})\)` -- * `\(\Large \sum(y − \bar{y})^2 = \sum(\hat{y} − \bar{y})^2 + \sum(y − \hat{y})^2\)` -- * ## SSTotal = SSModel + SSE --- # Degrees of freedom * ### SSTotal: `\(n-1\)` -- * ### SSE: `\(n-2\)` -- * ### SSModel: `\(n-1 = 1 + (n-2)\)` - so 1! 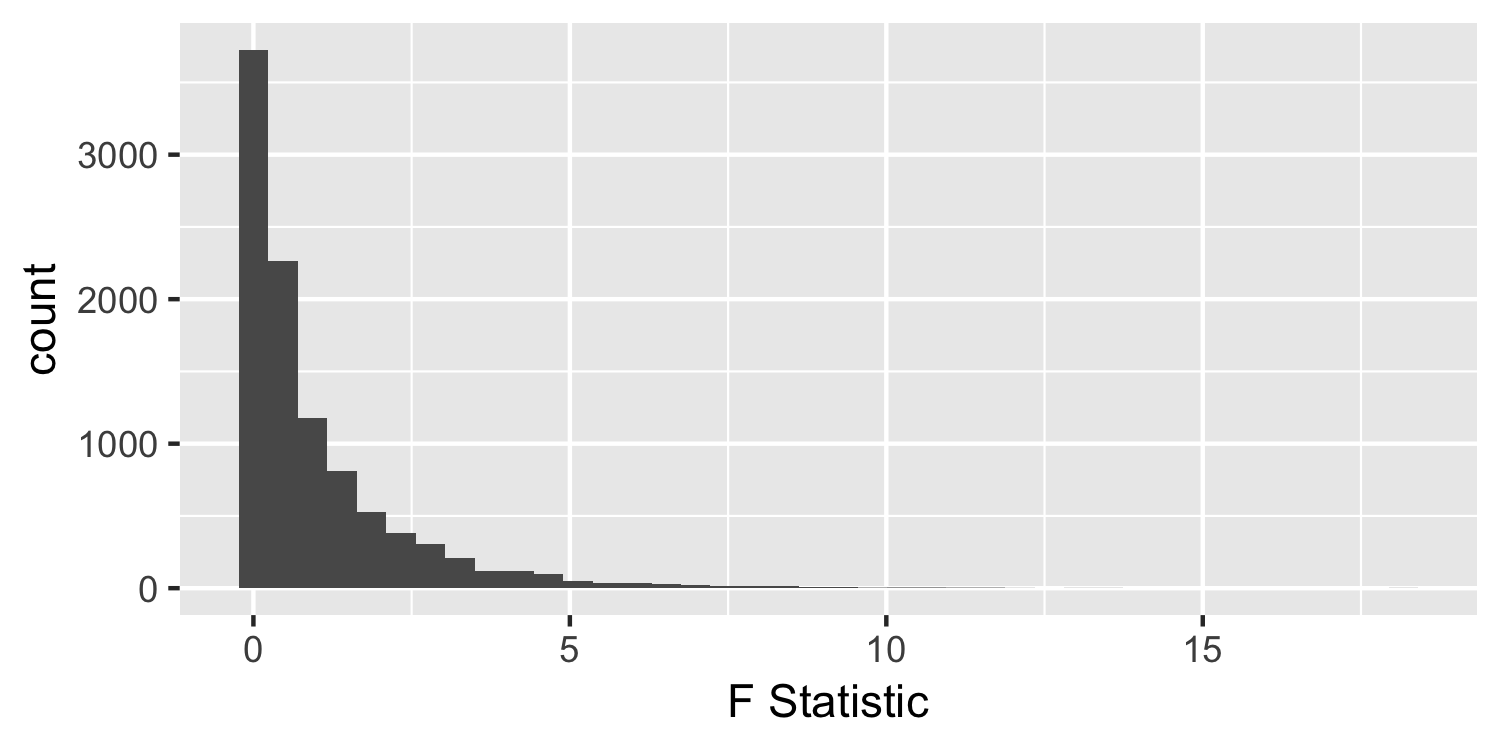--- # Mean Squares * `\(\Huge MSModel = \frac{SSModel}{1}\)` -- * `\(\Huge MSE = \frac{SSE}{n-2}\)` --- class: middle, center `\(\Huge F = \frac{MSModel}{MSE}\)` --- ## F-distribution Under the **null hypothesis** <!-- --> --- ## Sparrows We can see all of these pieces using the `anova()` function ```r lm(Weight ~ WingLength, data = Sparrows) %>% anova() ``` ``` ## Analysis of Variance Table ## ## Response: Weight ## Df Sum Sq Mean Sq F value Pr(>F) ## WingLength 1 355.05 355.05 181.25 < 2.2e-16 ## Residuals 114 223.31 1.96 ``` --- ## Sparrows .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] -- * F-statistic: 181.25 -- * p-value: 2.62e-25 -- * Where did this p-value come from? 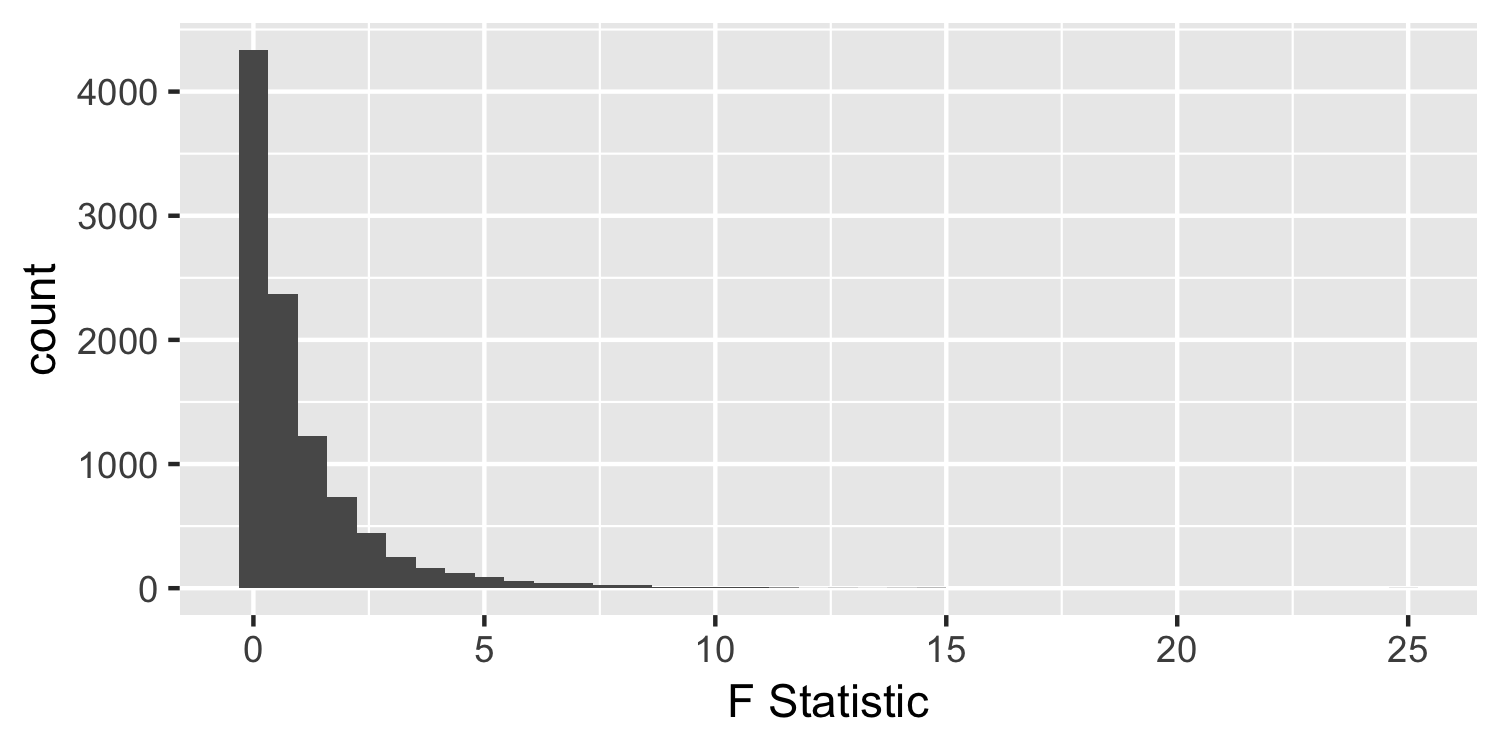--- class: middle # p-value The probability of getting a statistic as extreme or more extreme than the observed test statistic **given the null hypothesis is true** --- ## F-distribution Under the **null hypothesis** <!-- --> --- ## Sparrows: Degrees of freedom * SSTotal: `\(n-1\)` = 115 -- * SSE: ? -- * SSModel: ? --- ## Sparrows: Degrees of freedom * SSTotal: `\(n-1\)` = 115 -- * SSE: `\(n-2\)` = 114 -- * SSModel: 115 - 114 = 1 --- ## Sparrows .question[ To calculate the p-value under the **t-distribution** we used `pt()`. What do you think we use to calculate the p-value under the **F-distribution**? ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] --- ## Sparrows .question[ To calculate the p-value under the **t-distribution** we used `pt()`. What do you think we use to calculate the p-value under the **F-distribution**? ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] * `pf()` -- * it takes 3 arguments: `q`, `df1`, and `df2`. What do you think `df1` and `df2` are? --- ## Sparrows .question[ To calculate the p-value under the **t-distribution** we used `pt()`. What do you think we use to calculate the p-value under the **F-distribution**? ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] ```r pf(181.2535, 1, 114, lower.tail = FALSE) ``` ``` ## [1] 2.621946e-25 ``` --- ## Sparrows .question[ Why don't we multiple this p-value by 2 when we use `pf()`? ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. 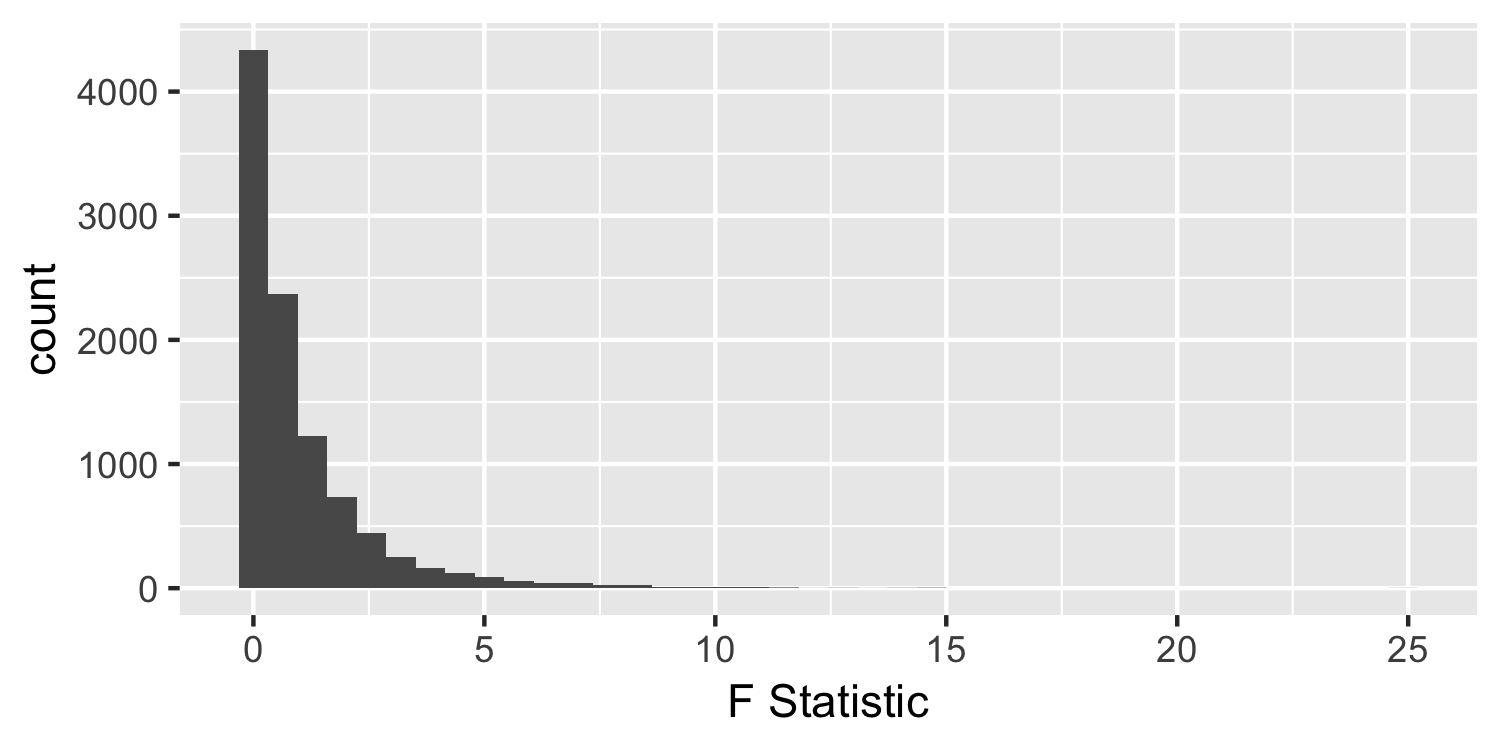## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] ```r pf(181.2535, 1, 114, lower.tail = FALSE) ``` ``` ## [1] 2.621946e-25 ``` --- ## F-Distribution Under the **null hypothesis** <!-- --> * We observed an F-statistic of 181.25, but for demonstration purposes, let's assume we saw one of 2. 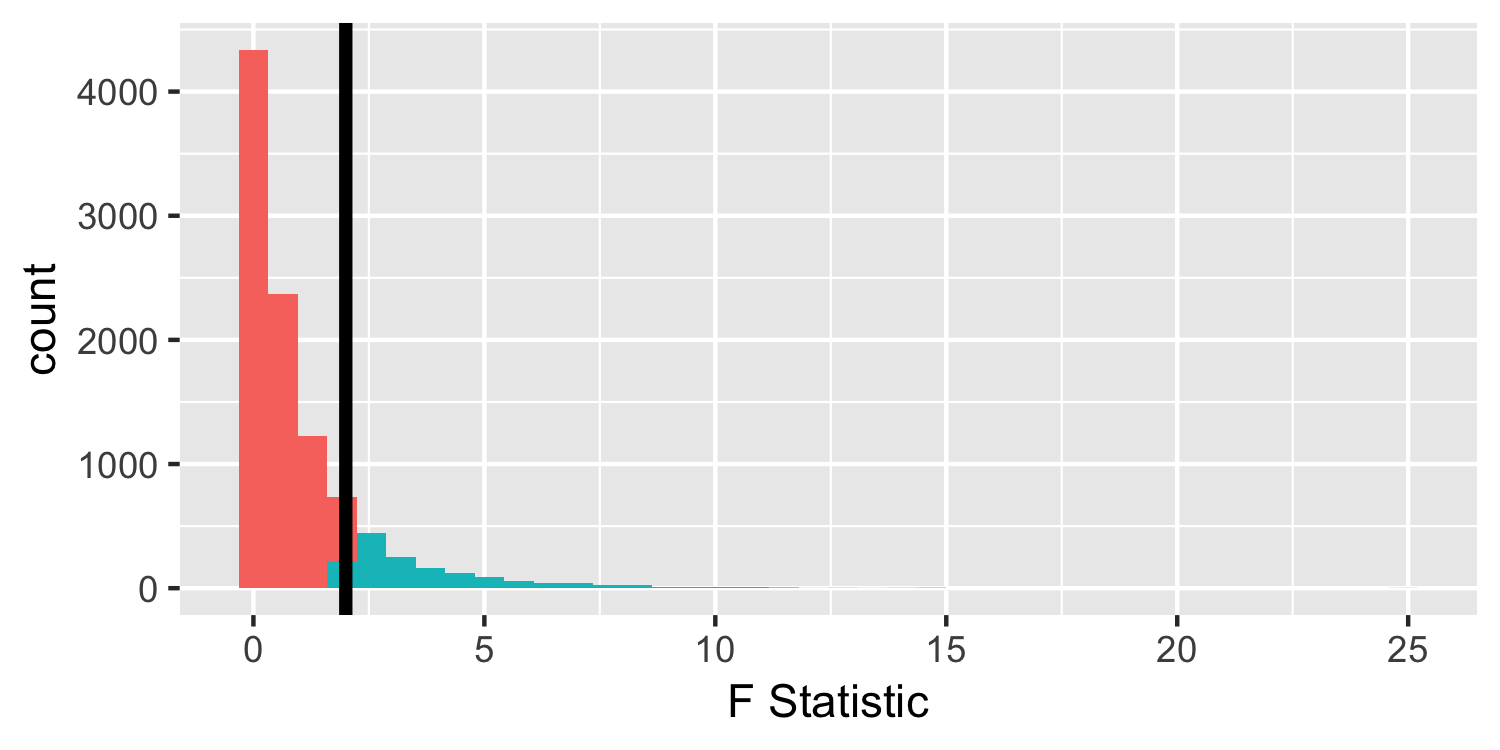--- ## F-Distribution Under the **null hypothesis** <!-- --> * We observed an F-statistic of 181.25, but for demonstration purposes, let's assume we saw one of 2. 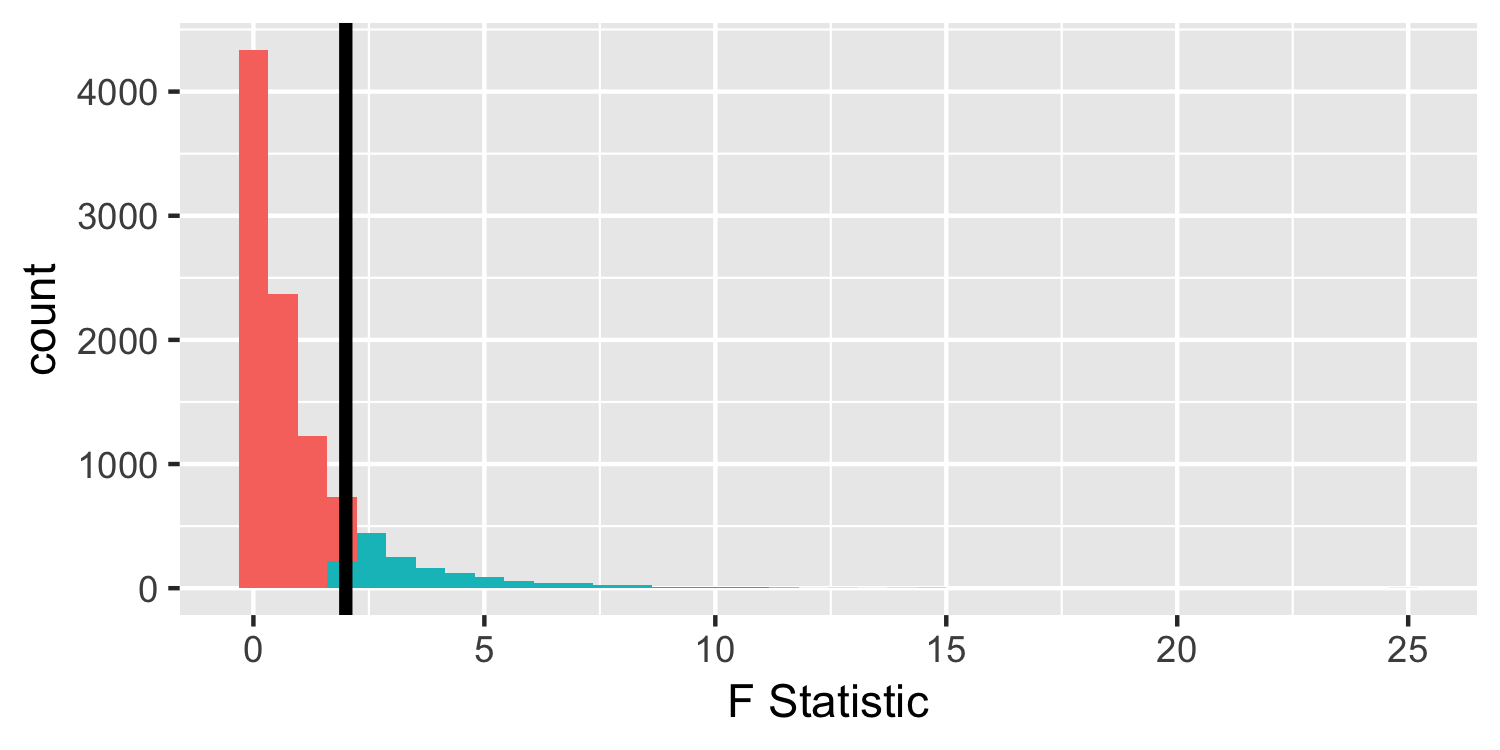--- ## F-Distribution Under the **null hypothesis** <!-- --> * Are there any negative values in an F-distribution? 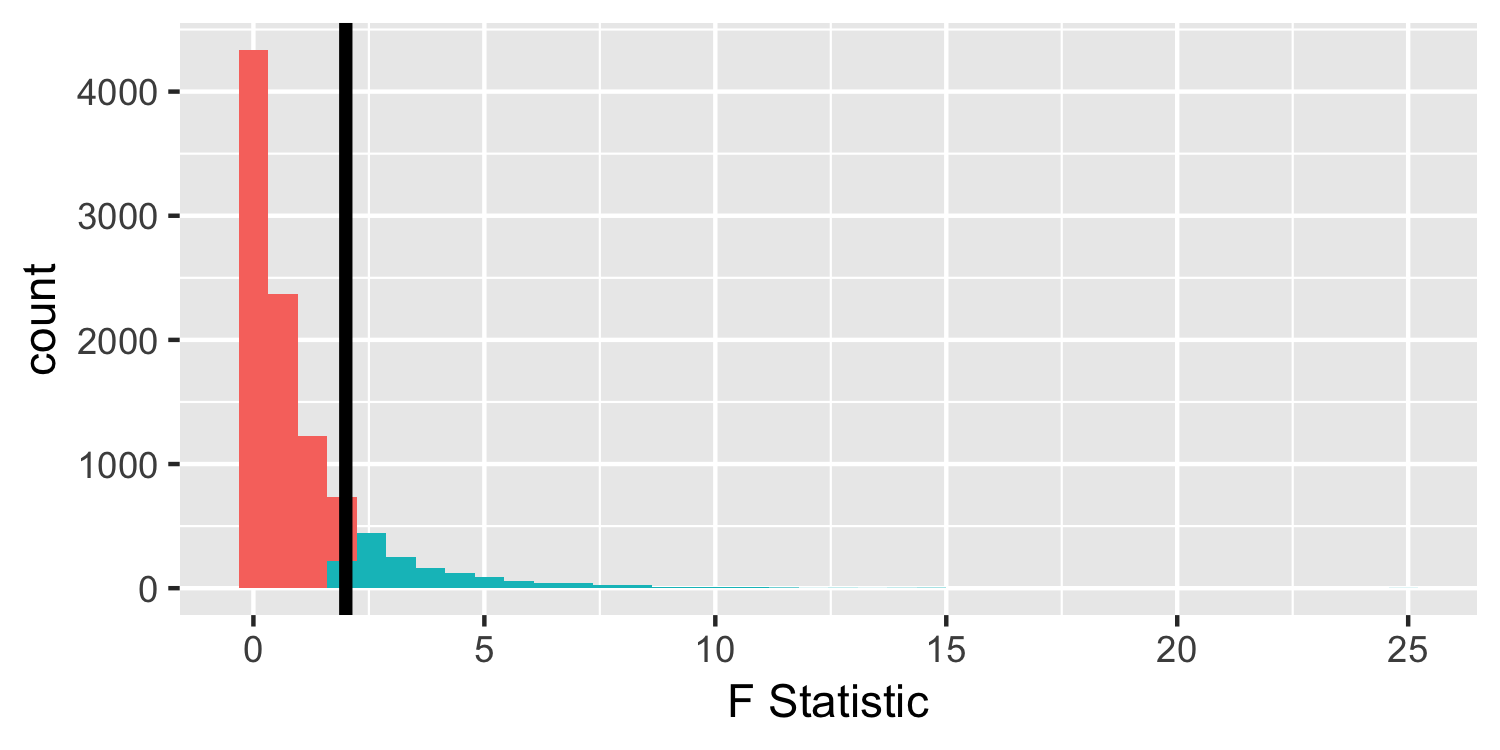--- ## F-Distribution Under the **null hypothesis** <!-- --> * The p-value calculates values "as extreme or more extreme", in the **t-distribution** "more extreme values", defined as farther from 0, can be positive **or** negative. Not so for the F! --- ## Sparrows ### Notice the p-value for the F-test is the same as the p-value for the t-test for `\(\beta_1\)`! .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> *## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% tidy() ``` ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 *## 2 WingLength 0.467 0.0347 13.5 2.62e-25 ``` ] --- ## Sparrows .question[ What is the F-test testing? ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> ## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] -- * **null hypothesis**: the fit of the **intercept only model** (with `\(\hat\beta_0\)` only) and your model (in this case, `\(\hat\beta_0 + \hat\beta_1x\)` ) are equivalent -- * **alternative hypothesis**: The fit of the intercept only model is significantly worse compared to your model -- * When we only have one variable in our model, `\(x\)`, the p-values from the F and t are going to be equivalent --- ## Sparrows .small[ .question[ How are the test statistics related between the F and the t? ] ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% glance() ``` ``` ## # A tibble: 1 x 11 ## r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC ## <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> *## 1 0.614 0.611 1.40 181. 2.62e-25 2 -203. 411. 419. ## # … with 2 more variables: deviance <dbl>, df.residual <int> ``` ] .small[ ```r lm(Weight ~ WingLength, data = Sparrows) %>% tidy() ``` ``` ## # A tibble: 2 x 5 ## term estimate std.error statistic p.value ## <chr> <dbl> <dbl> <dbl> <dbl> ## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 *## 2 WingLength 0.467 0.0347 13.5 2.62e-25 ``` ] -- .pull-left[ ```r 13.5^2 ``` ``` ## [1] 182.25 ``` ] .pull-right[ ``` ## [1] 182.25 ``` ]