Drawing inference
🤔
Porsche Price (3)
- Go to RStudio Cloud and open
Porsche Price (3)
in·fer·ence
a conclusion reached on the basis of evidence and reasoning.
Inference
- so far we've only been able to make claims about our sample
Inference
- so far we've only been able to make claims about our sample
- for example, we've just been describing ^β1, the estimated slope of the relationship between x and y.
Inference
- so far we've only been able to make claims about our sample
- for example, we've just been describing ^β1, the estimated slope of the relationship between x and y.
- what if we want to extend these claims to the population?
Sparrow data
So far, we've been looking at a sample of 116 sparrows from Kent Island.
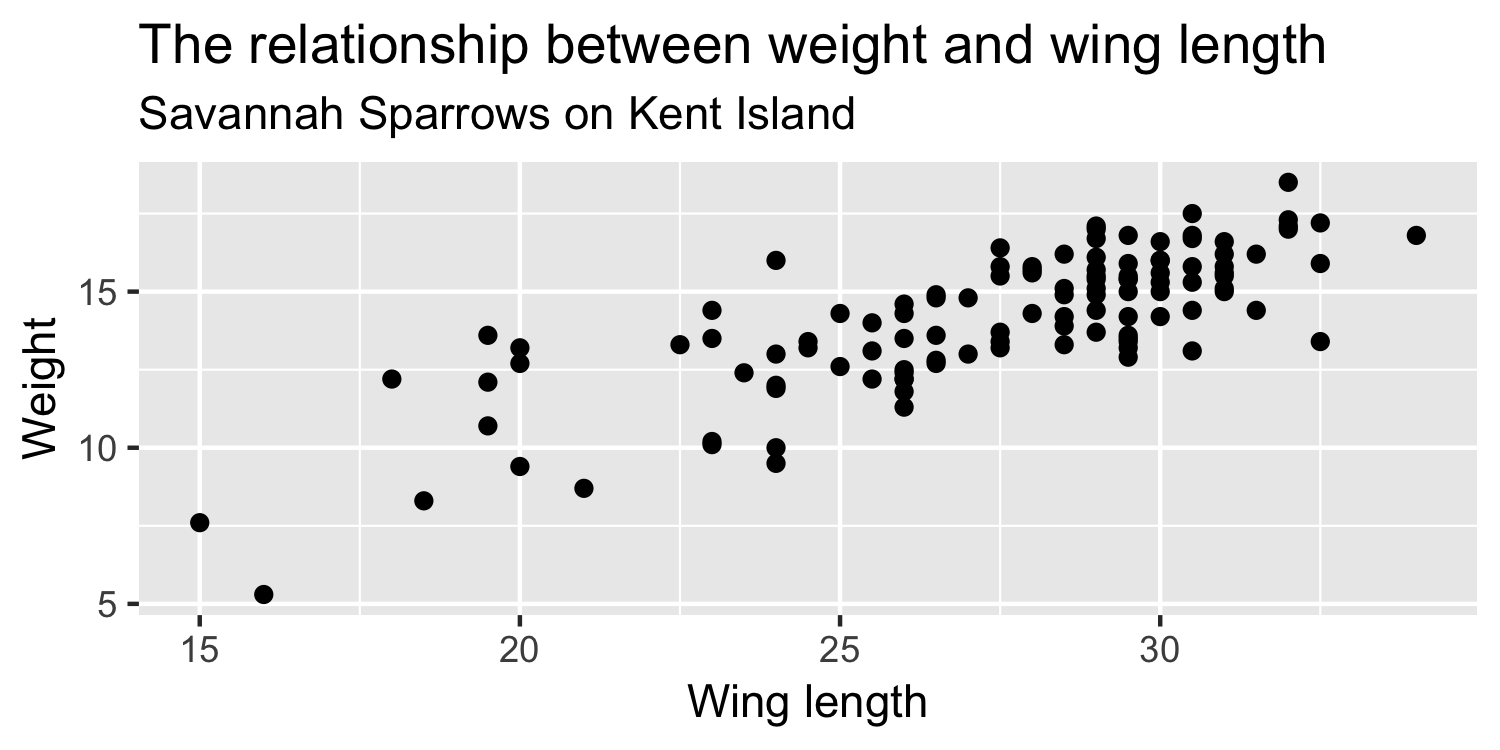
Sparrows
What if this were the true population, and the sample that we saw was just related by chance?
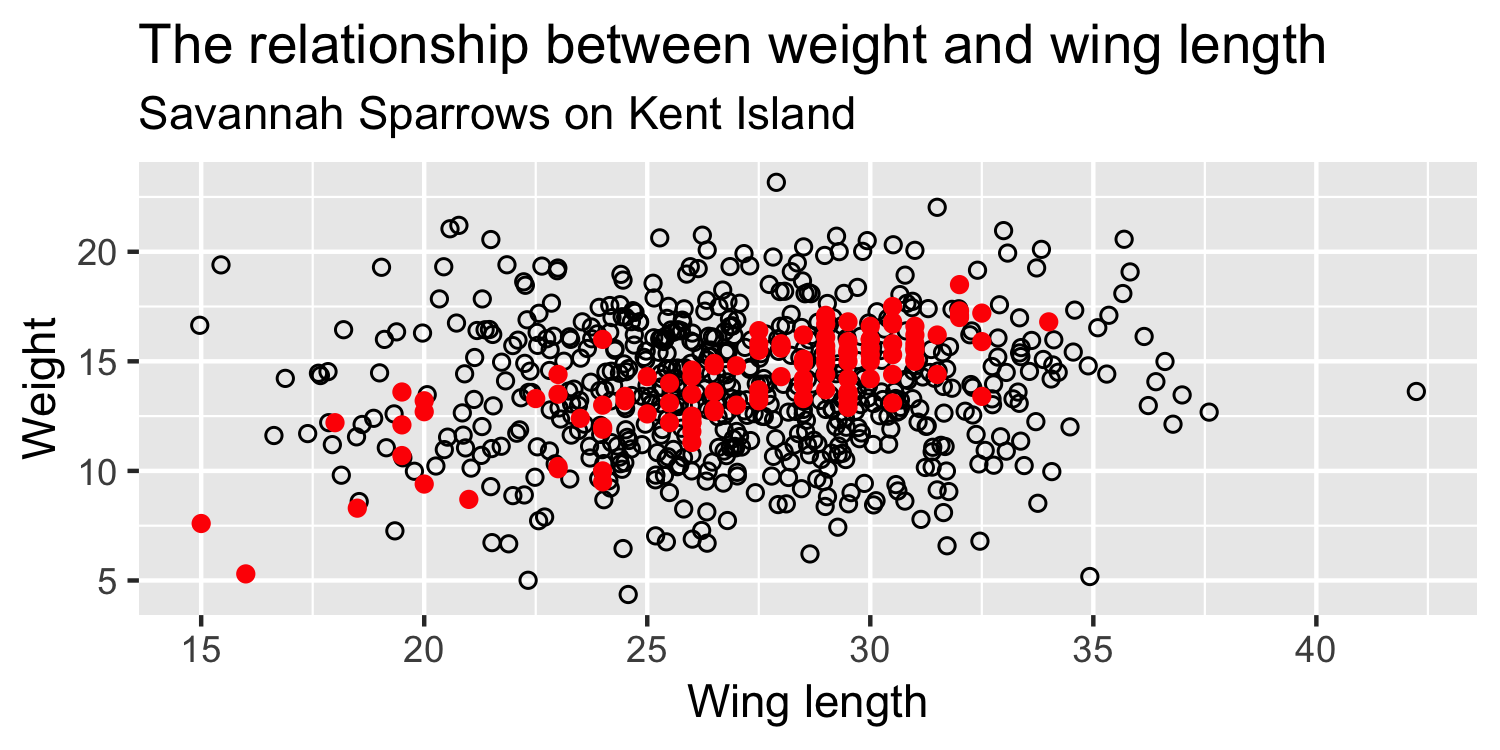
Sparrows
Ultimately What do we want to know?
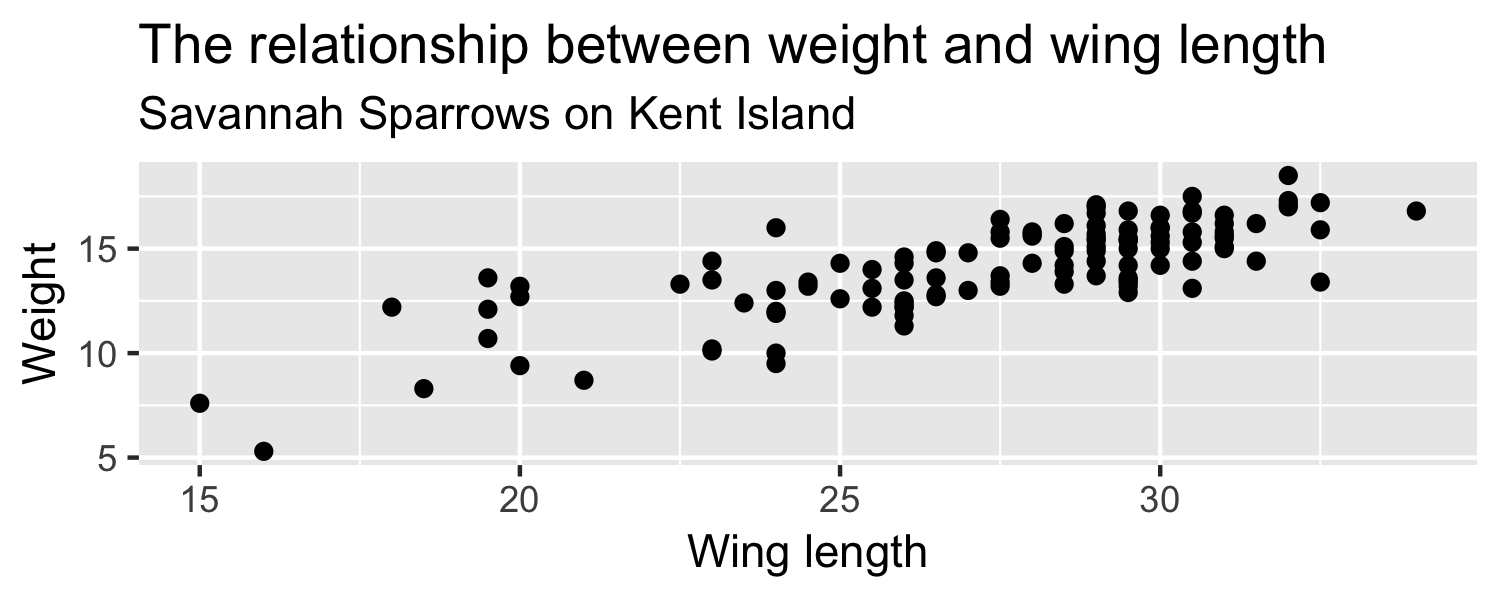
Sparrows
Ultimately What do we want to know?
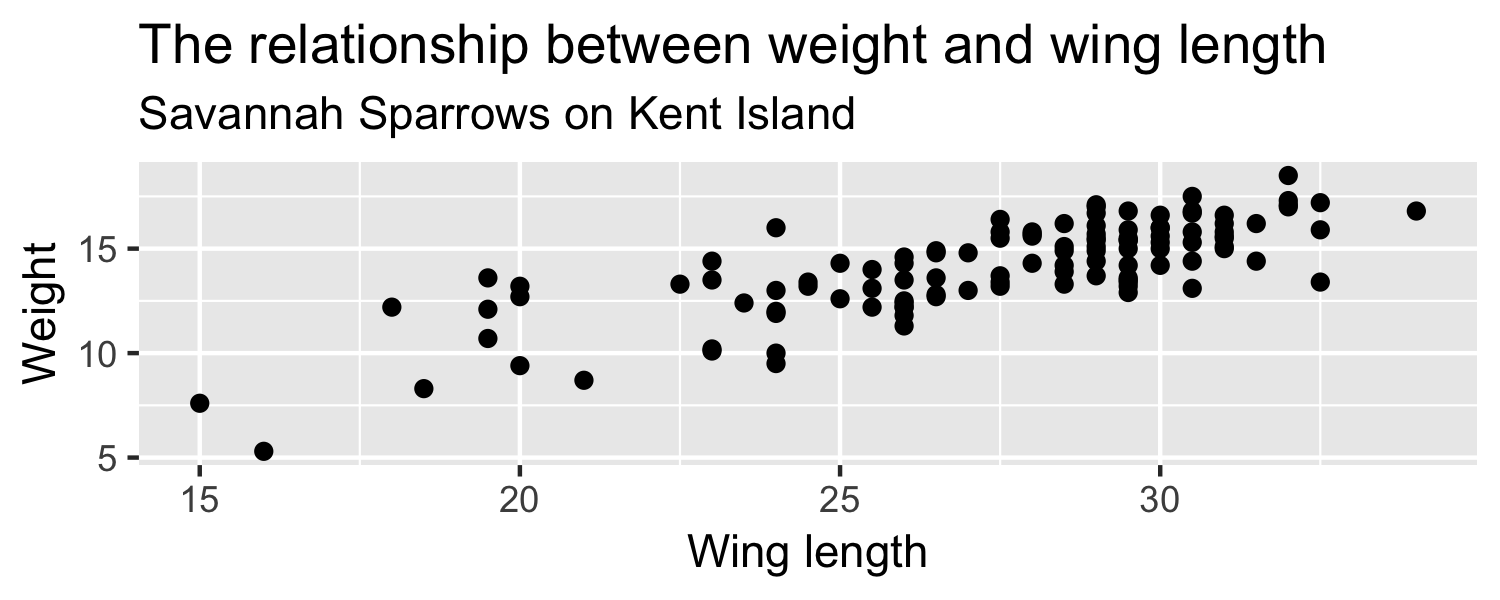
- Does the slope in the population differ from 0?
Sparrows
Ultimately What do we want to know?
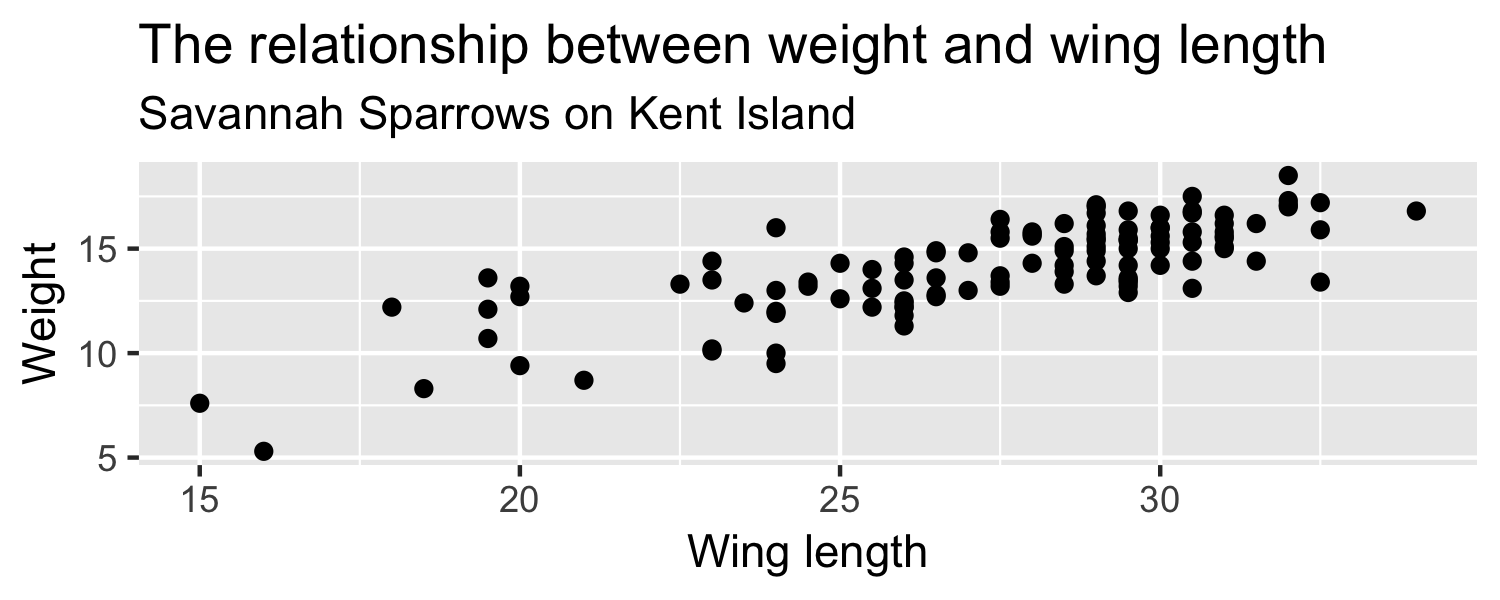
- Does β1 differ from 0?
Sparrows
Ultimately What do we want to know?

- Does β1 differ from 0?
- notice the lack of a hat!
Sparrows
Ultimately What do we want to know?
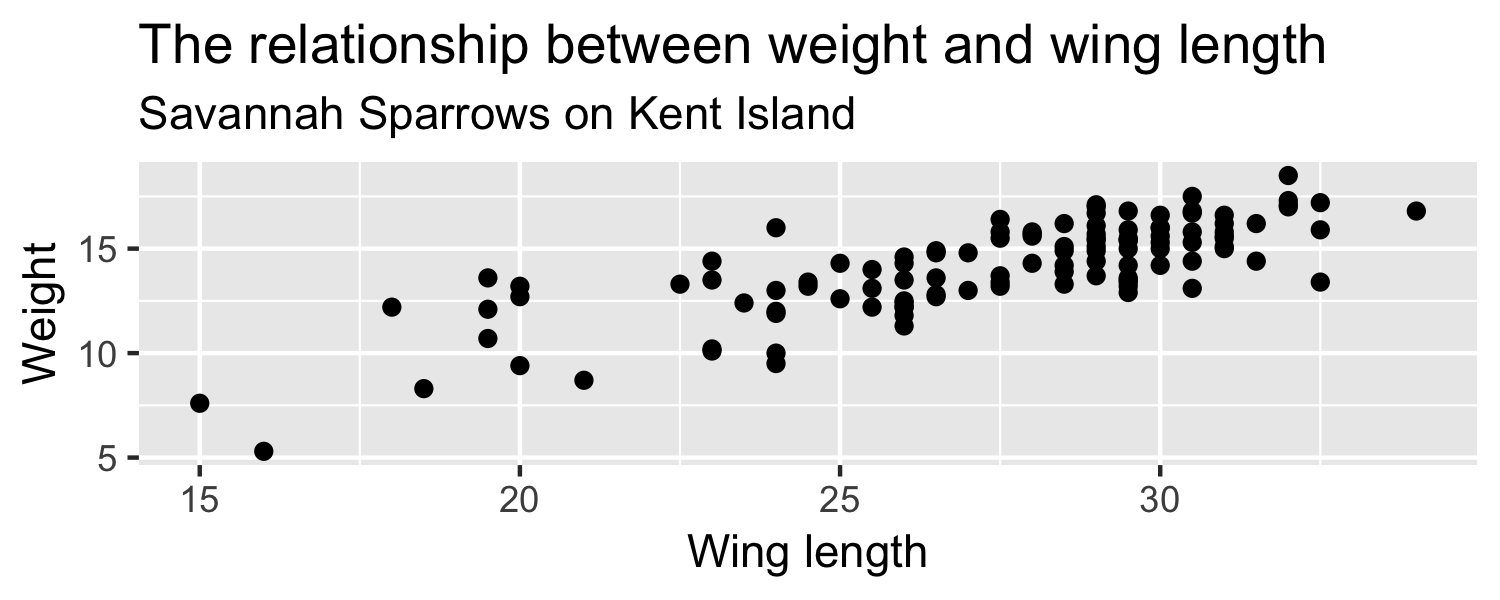
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0
Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
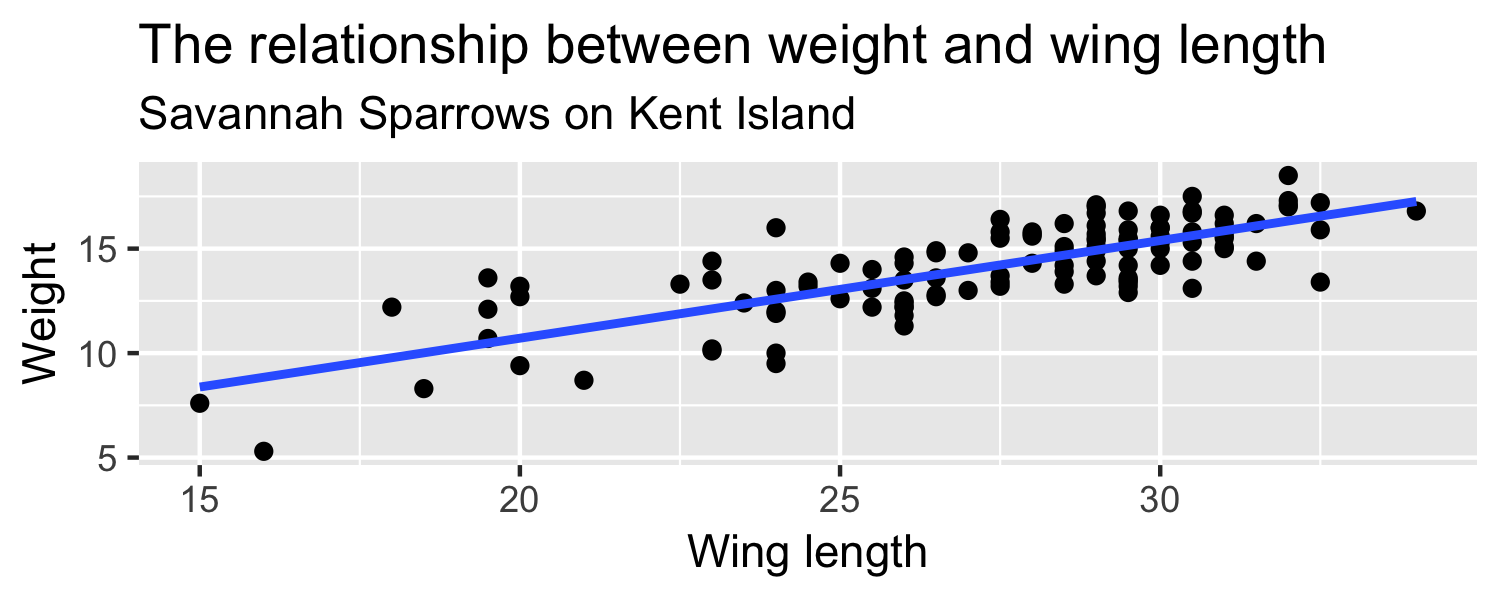
Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
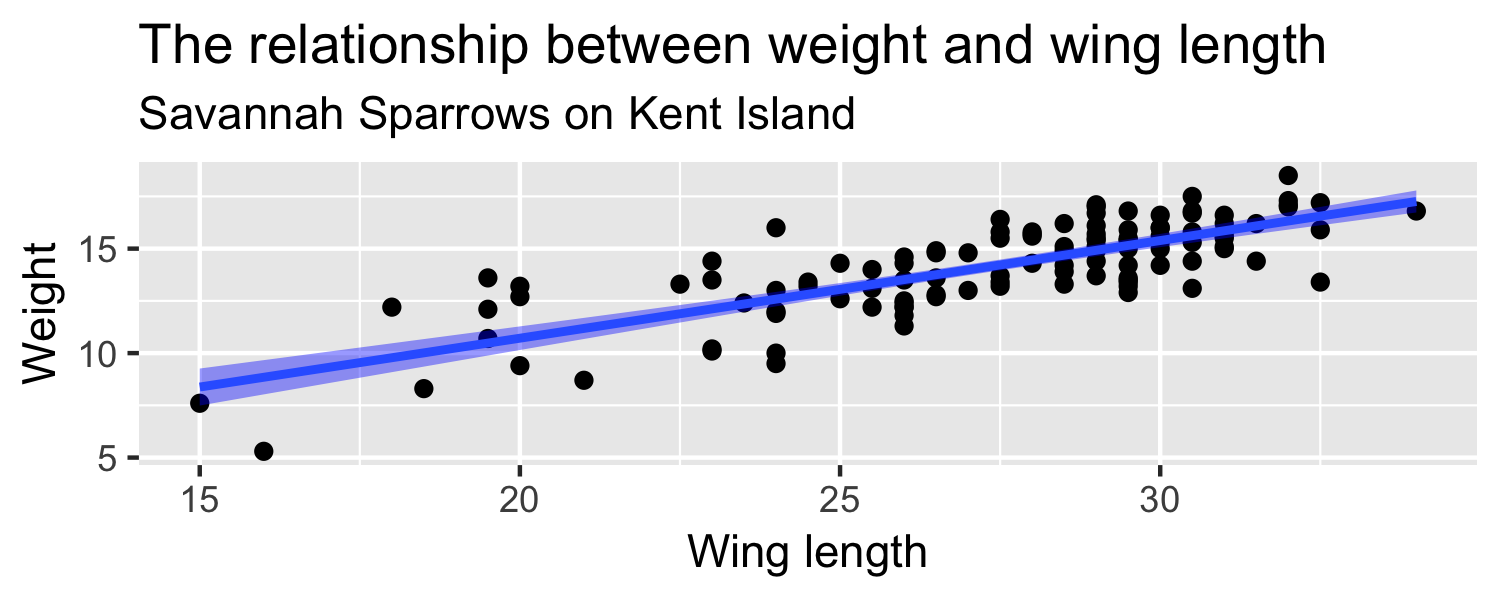
- We need a measure of uncertainty
Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
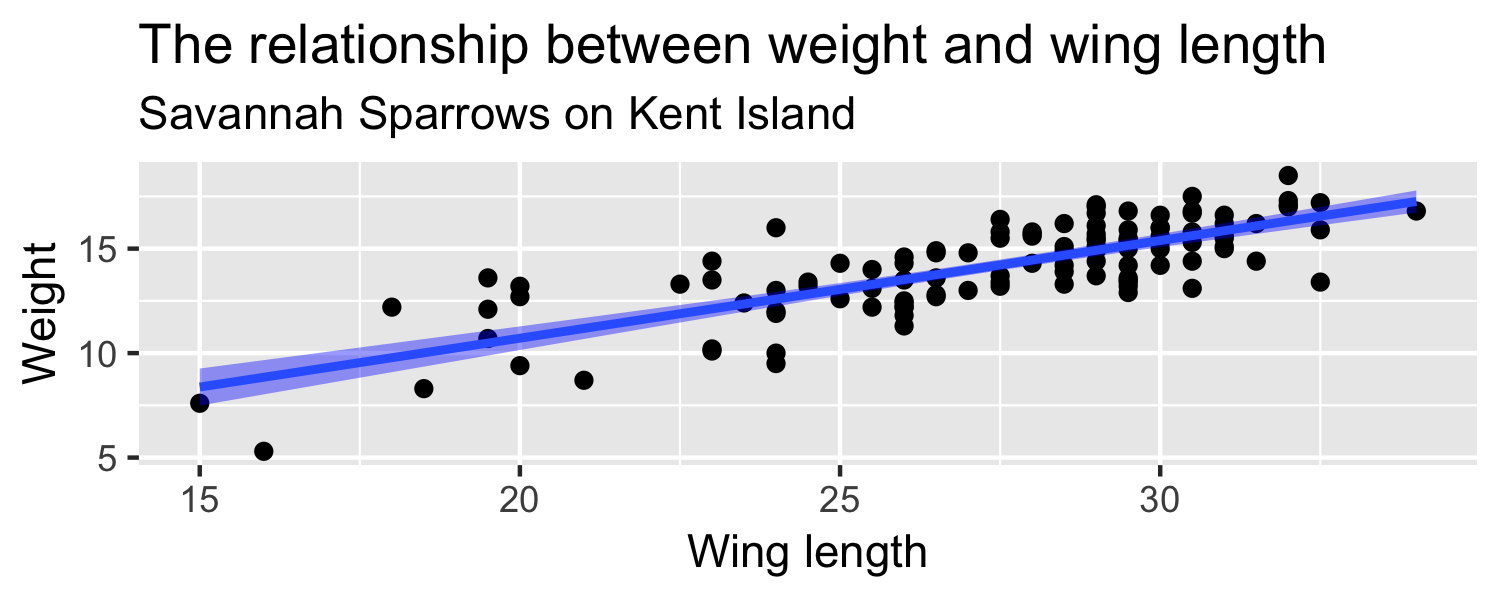
- How about the standard error of ^β1?
Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
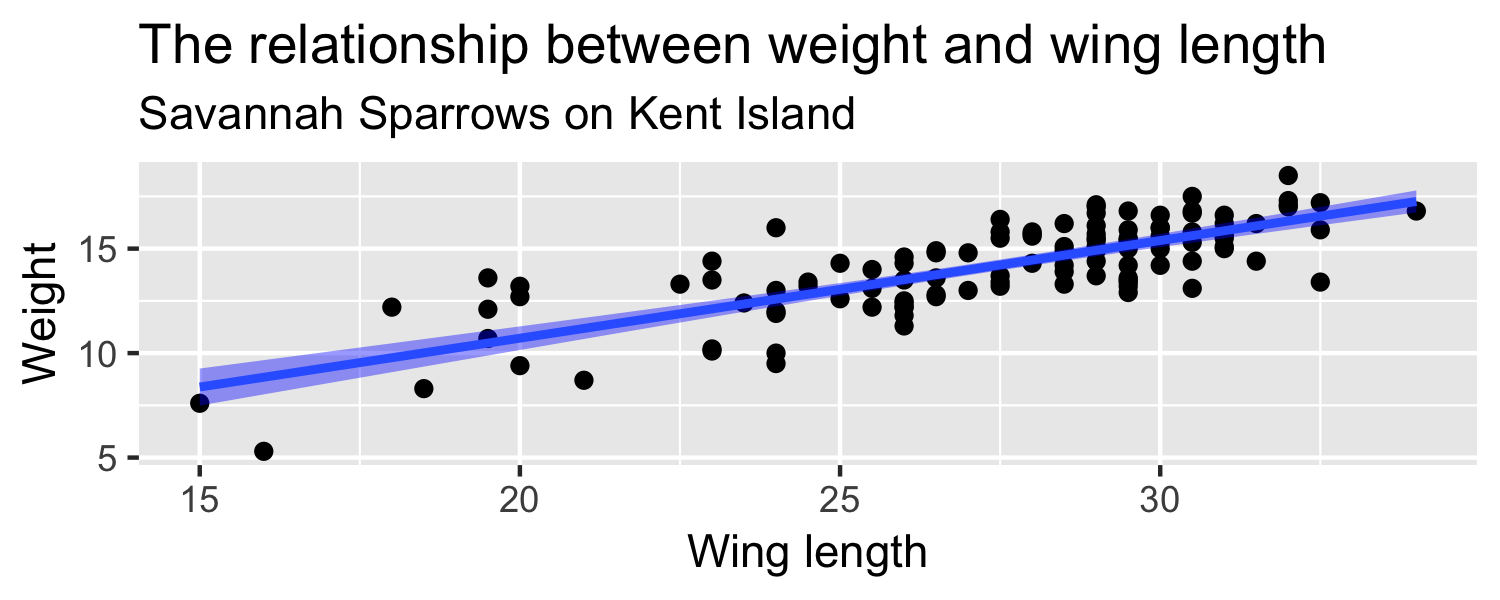
- the standard error of ^β1 ( SE^β1 ) is how much we expect the sample slope to vary from one random sample to another.
Sparrows
How can we quantify how much we'd expect the slope to differ from one random sample to another?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
We need a test statistic that incorporates ^β1 and the standard error SE^β1
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
We need a test statistic that incorporates ^β1 and the standard error SE^β1
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25t=^β1SE^β1
Sparrows
We need a test statistic that incorporates ^β1 and the standard error SE^β1
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-250.467 / 0.0347## [1] 13.45821Sparrows
How do we interpret this?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-250.467 / 0.0347## [1] 13.45821Sparrows
How do we interpret this?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25- "the sample slope is more than 13 standard errors above a slope of zero"
Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25- confidence intervals
- p-values
Sparrows
How do we know what values of this statistic are worth paying attention to?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536- confidence intervals
- p-values
Sparrows
Where do these come from?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536- confidence intervals
- p-values
Sparrows
What if we knew what the distribution of the "statistic" would be under the null hypothesis?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
null_sparrow_data <- data.frame( WingLength = rnorm(10, 27, 4), Weight = rnorm(10, 14, 3))lm(Weight ~ WingLength, data = null_sparrow_data) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 6.17 3.55 1.74 0.121 ## 2 WingLength 0.334 0.129 2.58 0.0326Sparrows
null_sparrow_data <- data.frame( WingLength = rnorm(10, 27, 4), Weight = rnorm(10, 14, 3))lm(Weight ~ WingLength, data = null_sparrow_data) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 11.2 5.96 1.88 0.0968## 2 WingLength 0.0840 0.206 0.407 0.695Sparrows
null_sparrow_data <- data.frame( WingLength = rnorm(10, 27, 4), Weight = rnorm(10, 14, 3))lm(Weight ~ WingLength, data = null_sparrow_data) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 11.7 5.94 1.97 0.0846## 2 WingLength 0.121 0.223 0.543 0.602Sparrows
gen_null_stat <- function() { null_sparrow_data <- data.frame( WingLength = rnorm(10, 27, 4), Weight = rnorm(10, 14, 3) ) lm(Weight ~ WingLength, data = null_sparrow_data) %>% tidy() %>% filter(term == "WingLength") %>% select("statistic")}gen_null_stat()## # A tibble: 1 x 1## statistic## <dbl>## 1 -0.661Sparrows
gen_null_stat()## # A tibble: 1 x 1## statistic## <dbl>## 1 -0.422gen_null_stat()## # A tibble: 1 x 1## statistic## <dbl>## 1 0.536gen_null_stat()## # A tibble: 1 x 1## statistic## <dbl>## 1 -2.19Sparrows
null_stats <- map_df(1:10000, ~ gen_null_stat())Sparrows
null_stats <- map_df(1:10000, ~ gen_null_stat())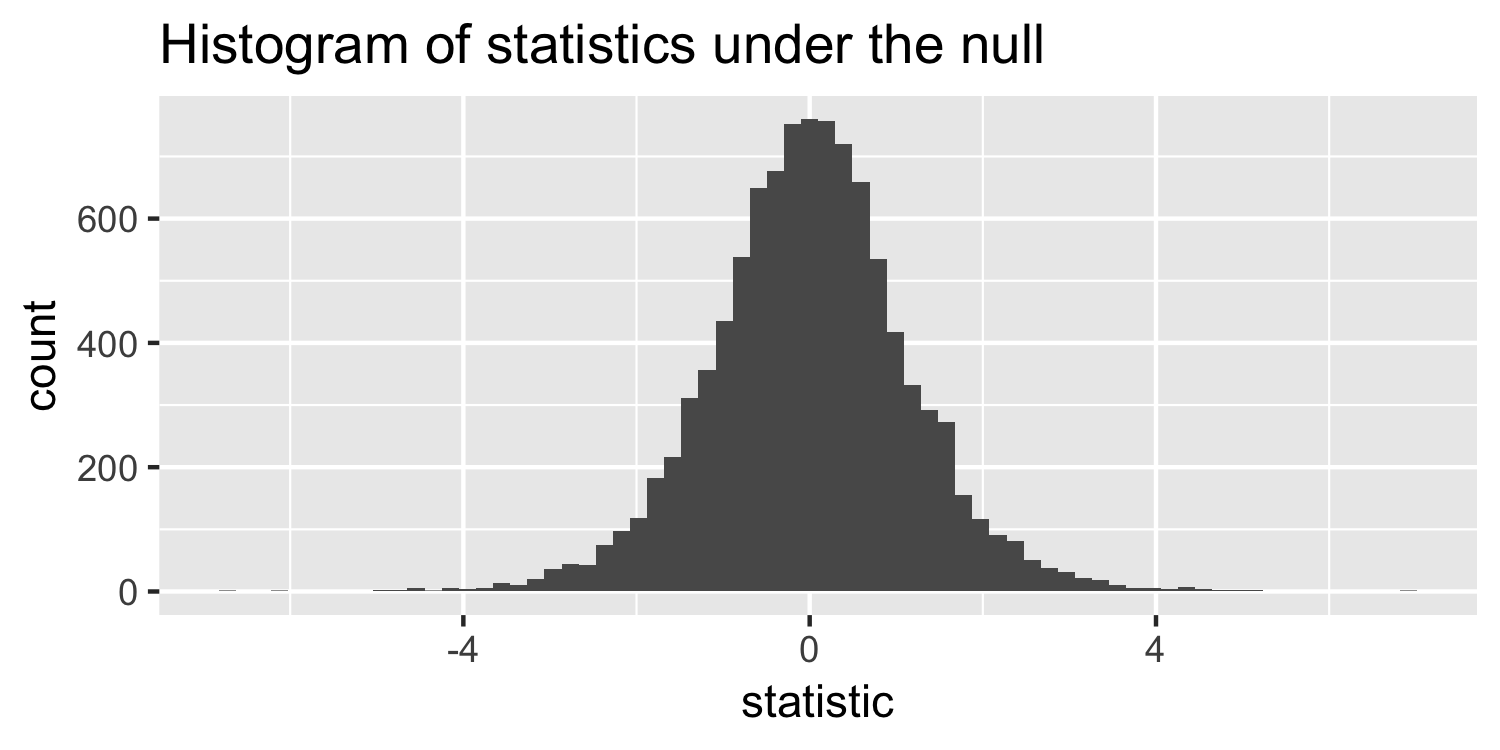
Sparrows
What distribution does this look like?
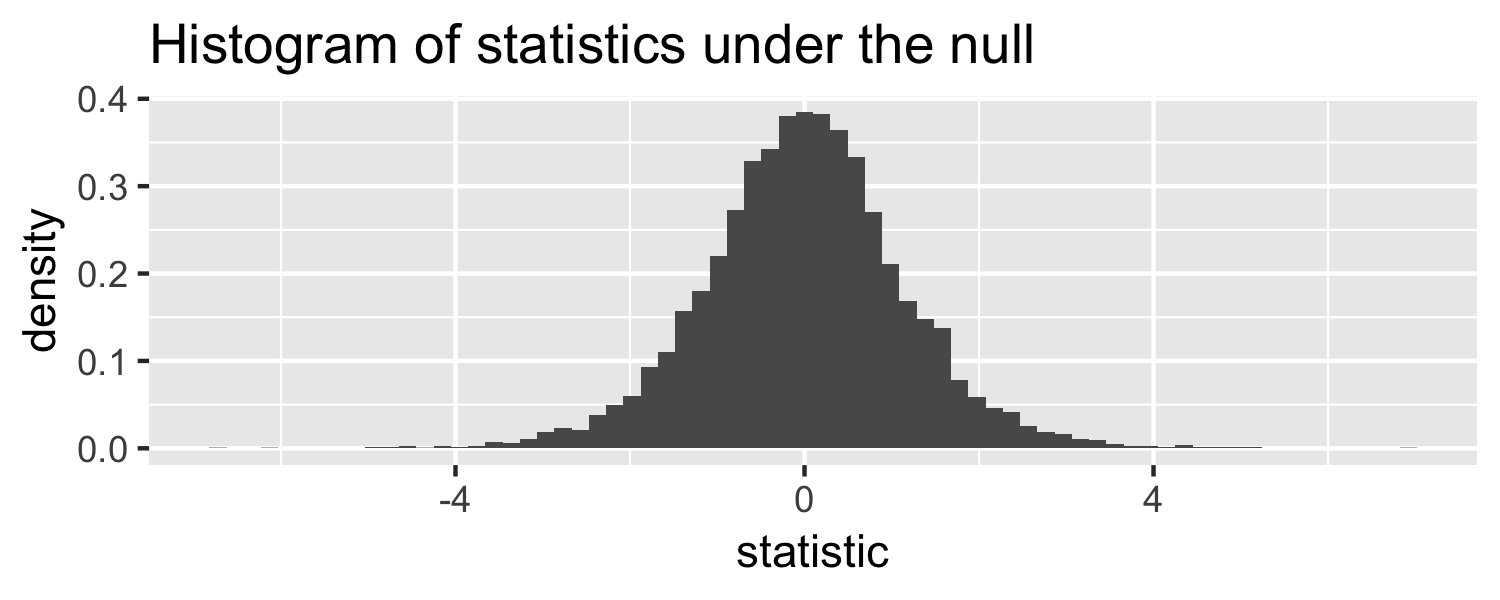
Sparrows
What distribution does this look like?
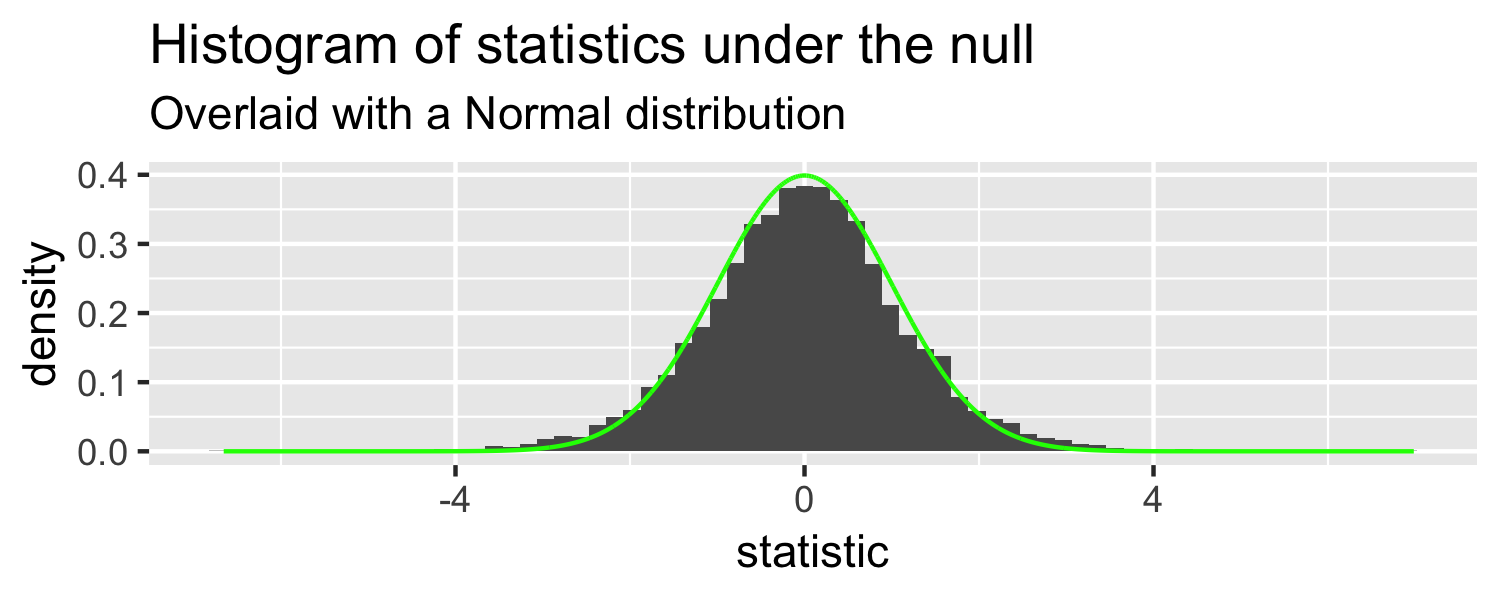
- Normal?
Sparrows
What distribution does this look like?

- Normal?
- What distribution is similar to the normal but with fatter tails?
Sparrows
What distribution does this look like?
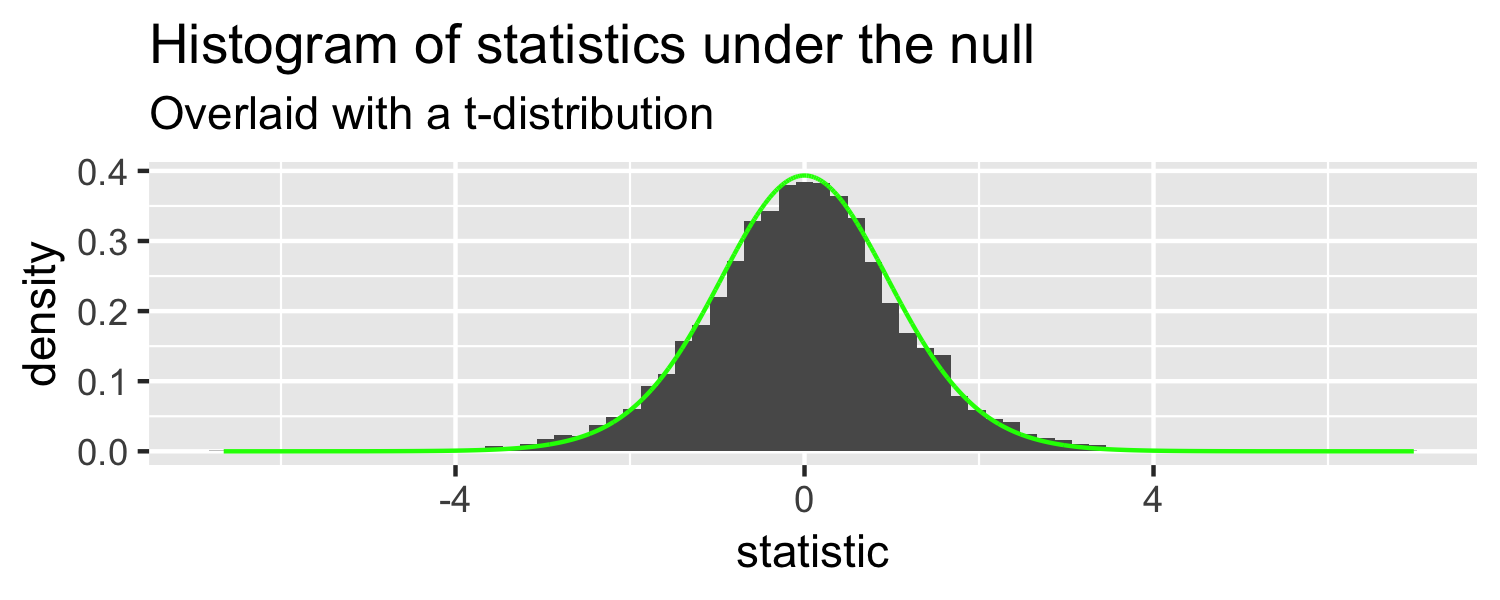
- the t-distribution!
Sparrows
What distribution does this look like?

- the t-distribution!
- this is a t-distribution with n-2 degrees of freedom.
Sparrows
The distribution of test statistics we would expect given the null hypothesis is true, β1=0, is t-distribution with n-2 degrees of freedom.
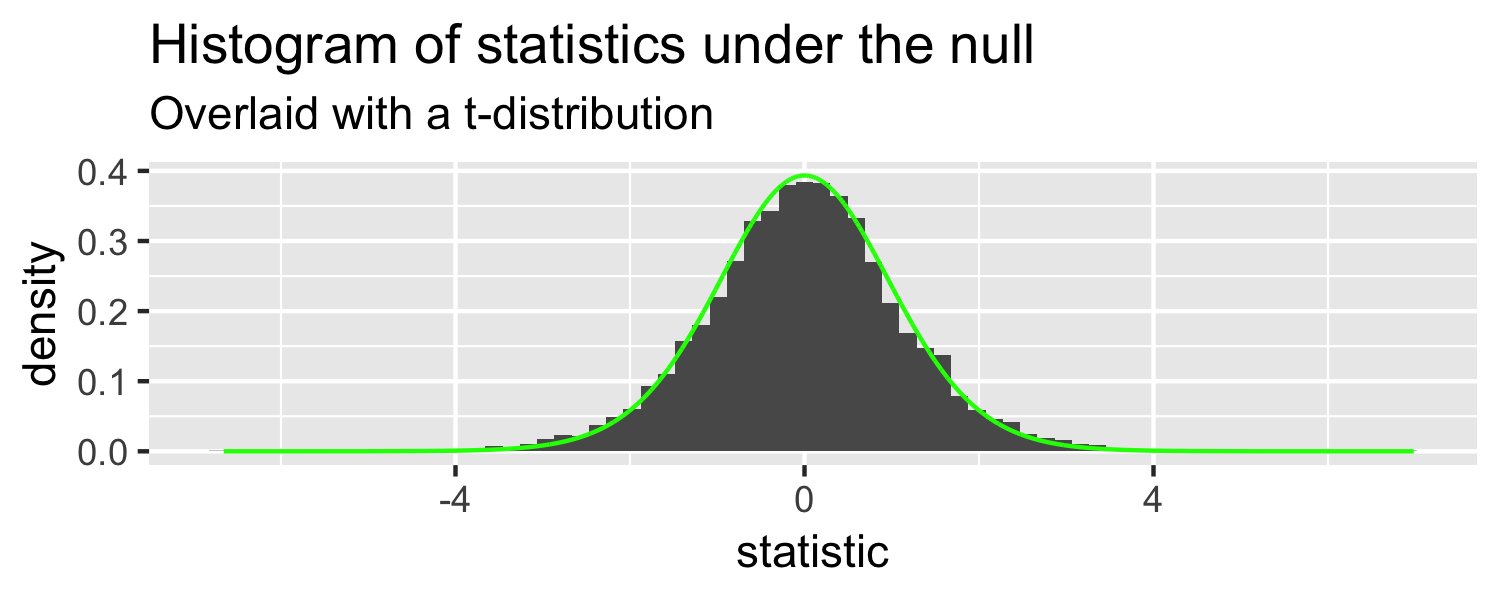
Sparrows
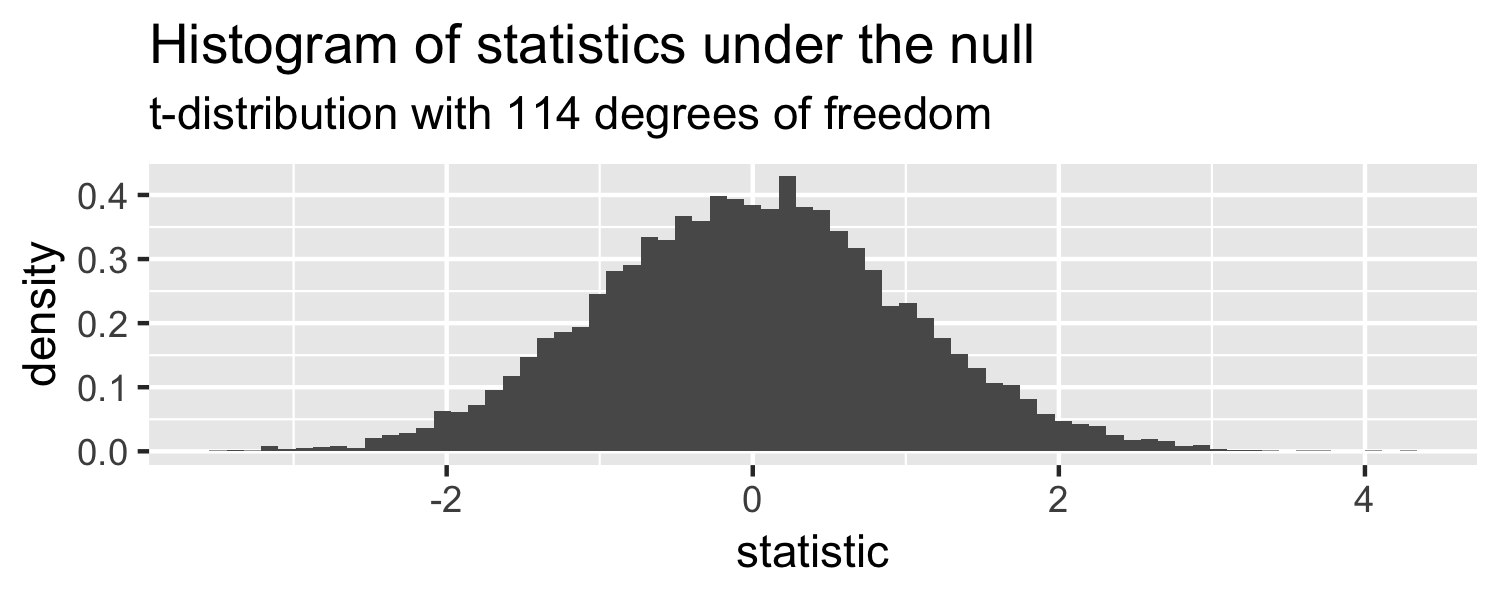
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Sparrows
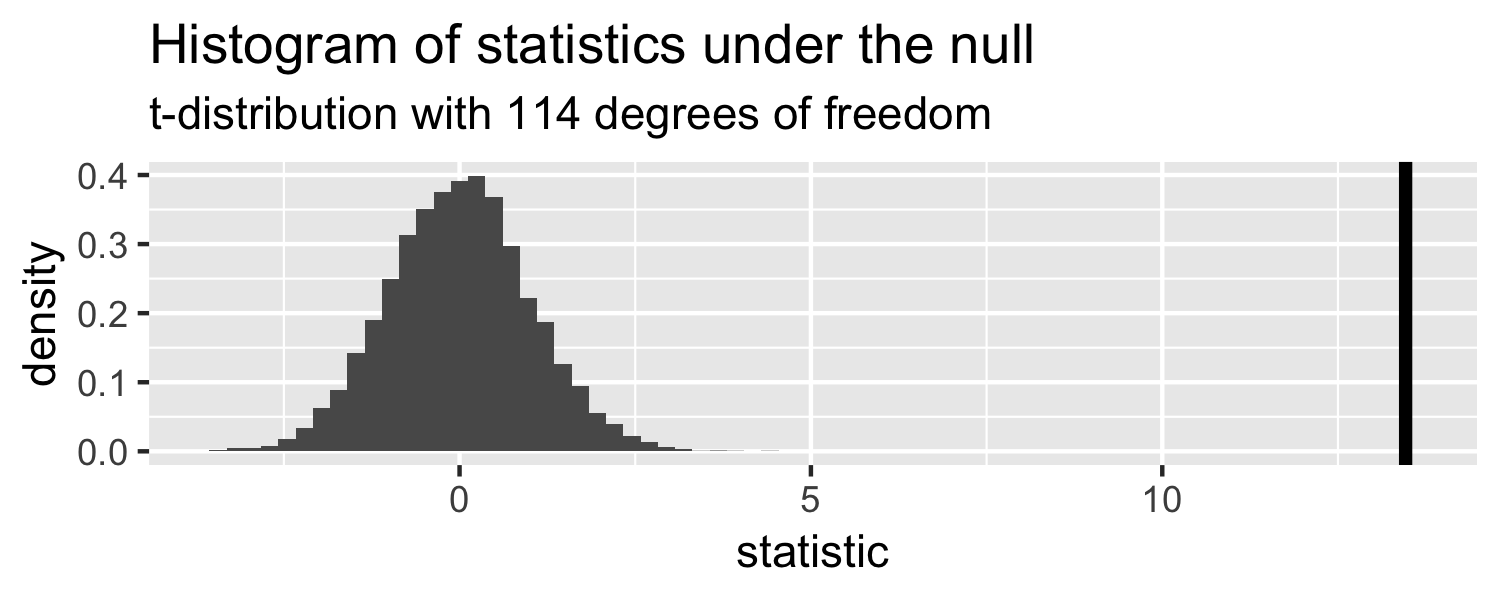
Sparrows
How can we compare this line to the distribution under the null?
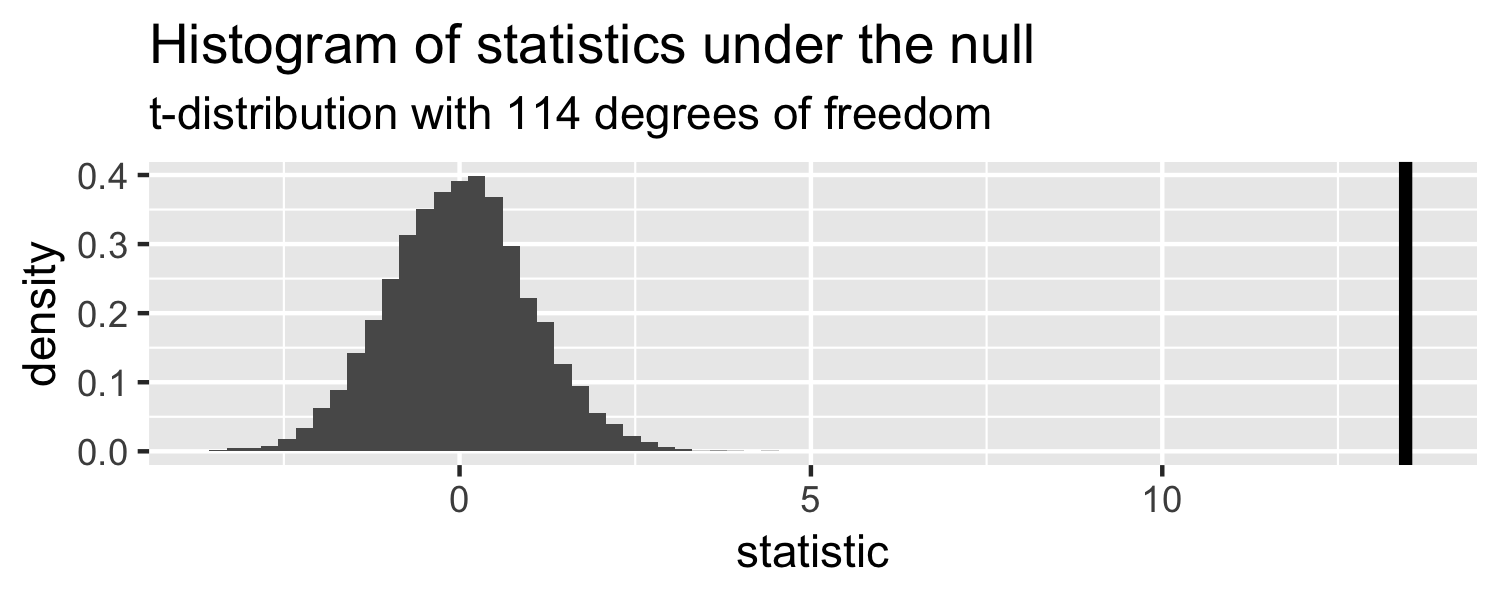
Sparrows
How can we compare this line to the distribution under the null?

- p-value
p-value
The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true
Sparrows
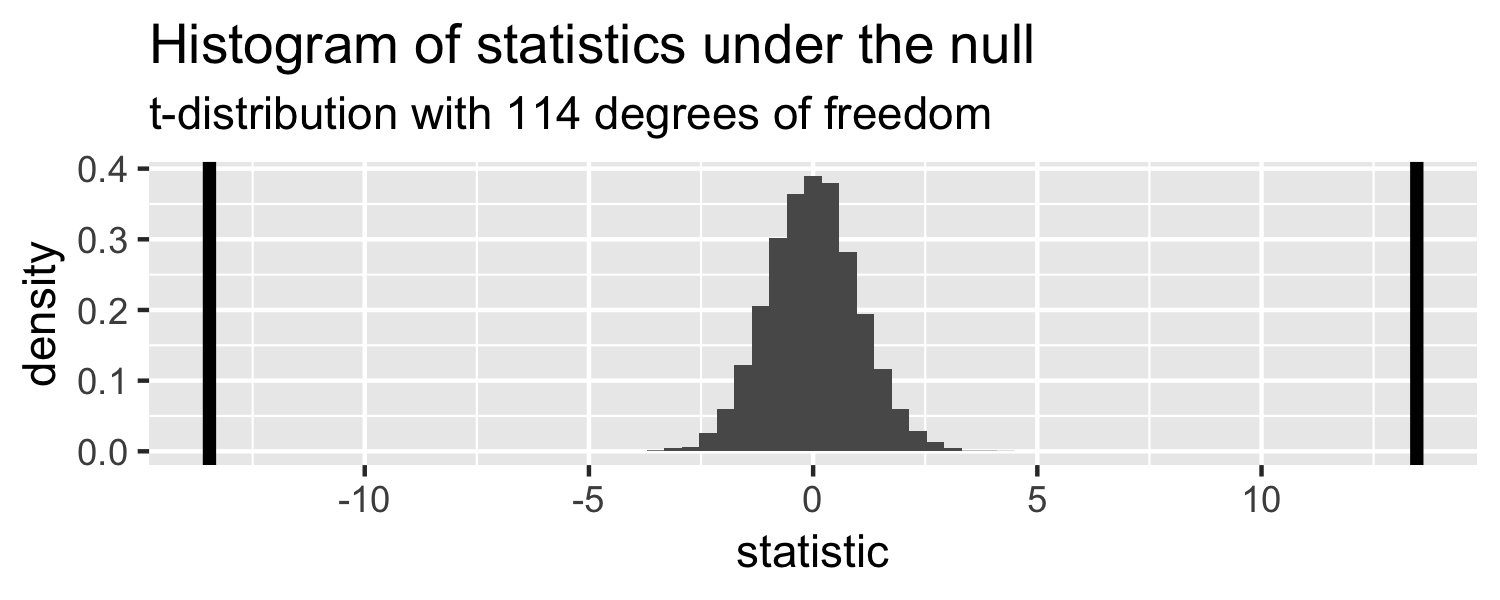
lm(Weight ~ WingLength, data = Sparrows) %>% tidy()## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1## 2 WingLength 0.467 0.0347 13.5 2.62e-25Return to generated data, n = 20
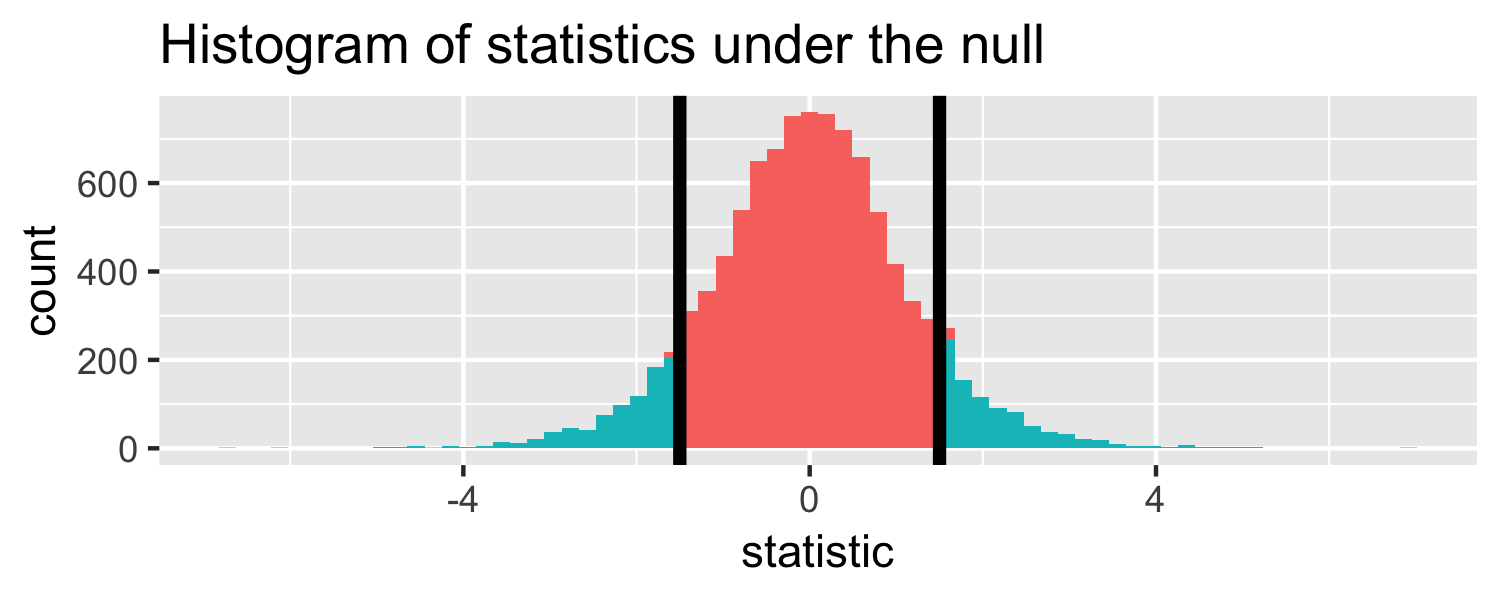
- Let's say we get a statistic of 1.5 in a sample
Let's do it in R!
The proportion of area less than 1.5
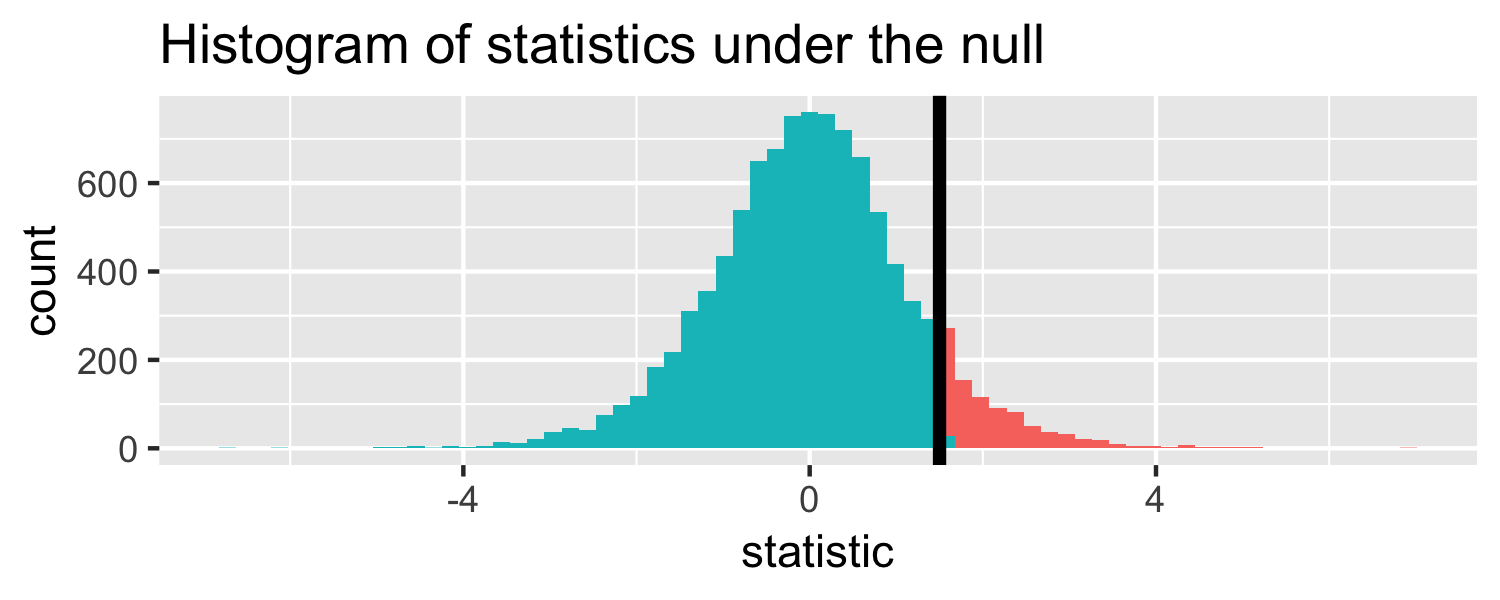
pt(1.5, df = 18)## [1] 0.9245248Let's do it in R!
The proportion of area greater than 1.5
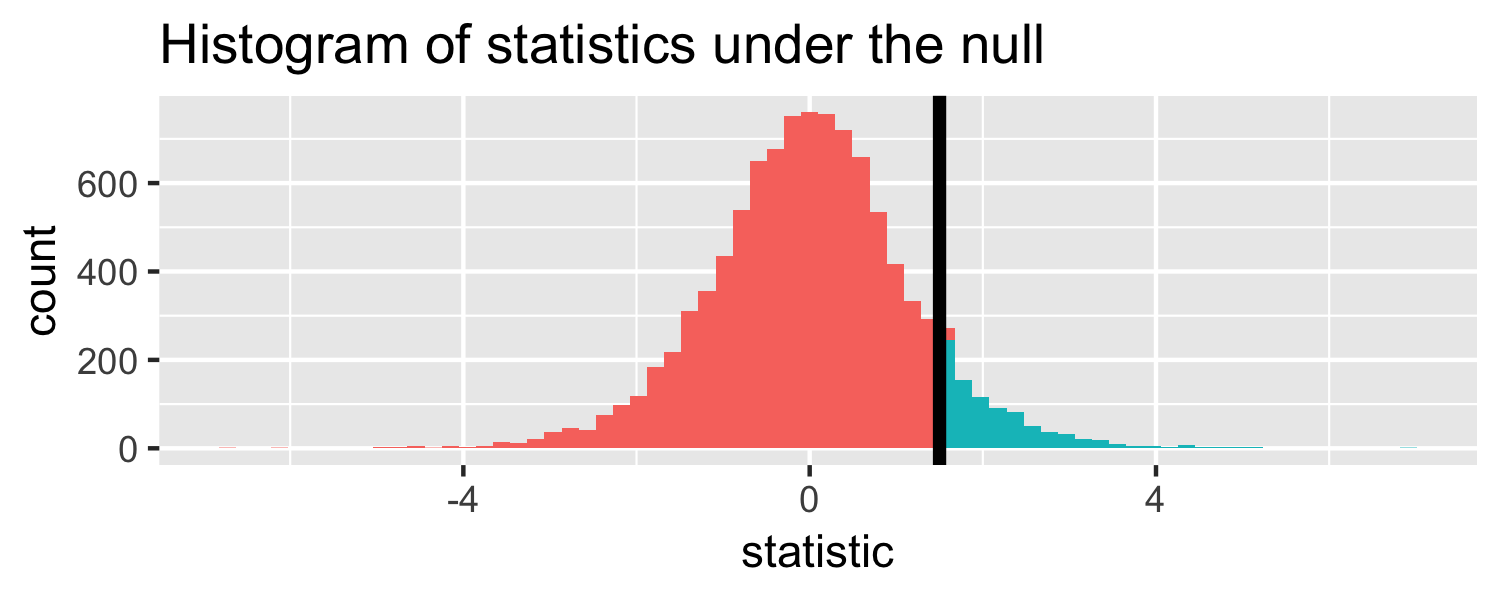
pt(1.5, df = 18, lower.tail = FALSE)## [1] 0.07547523Let's do it in R!
The proportion of area greater than 1.5 or less than -1.5.
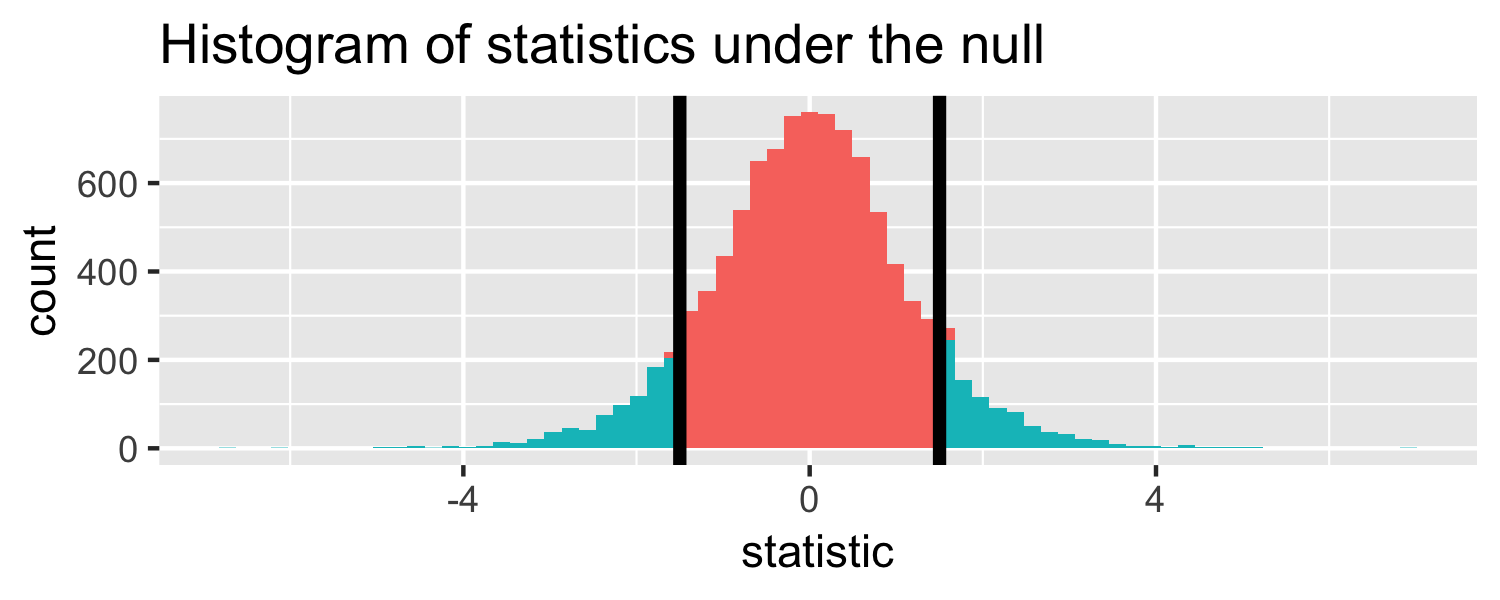
Let's do it in R!
The proportion of area greater than 1.5 or less than -1.5.

pt(1.5, df = 18, lower.tail = FALSE) * 2## [1] 0.1509505p-value
The probability of getting a statistic as extreme or more extreme than the observed test statistic given the null hypothesis is true
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0
- p-value: 0.15
Hypothesis test
- null hypothesis H0:β1=0
- alternative hypothesis HA:β1≠0
- p-value: 0.15
- Often, we have an α-level cutoff to compare this to, for example 0.05. Since this is greater than 0.05, we fail to reject the null hypothesis
confidence intervals
If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( β1 ) to fall within the interval estimates 95% of the time.
Confidence interval
^β1±t∗×SE^β1
Confidence interval
^β1±t∗×SE^β1
- t∗ is the critical value for the tn−2 density curve to obtain the desired confidence level
Confidence interval
^β1±t∗×SE^β1
- t∗ is the critical value for the tn−2 density curve to obtain the desired confidence level
- Often we want a 95% confidence level.
Let's do it in R!
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536qt(0.025, df = nrow(Sparrows) - 2, lower.tail = FALSE)## [1] 1.980992Let's do it in R!
Why 0.025?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536qt(0.025, df = nrow(Sparrows) - 2, lower.tail = FALSE)## [1] 1.980992Let's do it in R!
Why lower.tail = FALSE?
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536qt(0.025, df = nrow(Sparrows) - 2, lower.tail = FALSE)## [1] 1.980992Let's do it in R!
lm(Weight ~ WingLength, data = Sparrows) %>% tidy(conf.int = TRUE)## # A tibble: 2 x 7## term estimate std.error statistic p.value conf.low conf.high## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 1.37 0.957 1.43 1.56e- 1 -0.531 3.26 ## 2 WingLength 0.467 0.0347 13.5 2.62e-25 0.399 0.536t_star <- qt(0.025, df = nrow(Sparrows) - 2, lower.tail = FALSE)0.467 + t_star * 0.0347## [1] 0.5360.467 - t_star * 0.0347## [1] 0.398confidence intervals
If we use the same sampling method to select different samples and computed an interval estimate for each sample, we would expect the true population parameter ( β1 ) to fall within the interval estimates 95% of the time.
Porsche Price (3)
- Go to RStudio Cloud and open
Porsche Price (3)