Simple linear regression
Porsche Price
- Go to RStudio Cloud and open
Porsche Price
Steps for modeling
Steps for modeling
Data = Model + Error
y=f(x)+ϵ
y=f(x)+ϵ
Simple linear regression
y=f(x)+ϵ
- y: continuous (quantitative) variable
properties of simple linear regression
y=f(x)+ϵ
- x: continuous (quantitative) variable
properties of simple linear regression
y=f(x)+ϵ
- f(x): a function that gives the mean value of y at any value of x
properties of simple linear regression
function: a function is the relationship between a set of inputs to a set of outputs
function: a function is the relationship between a set of inputs to a set of outputs
- For example, y=1.5+0.5x is a function where x is the input and y is the output
function: a function is the relationship between a set of inputs to a set of outputs
- For example, y=1.5+0.5x is a function where x is the input and y is the output
- If you plug in 2 for x: y=1.5+0.5×2→y=1.5+1→y=2.5
What function do you think we are using get the mean value of y with simple linear regression?
What function do you think we are using get the mean value of y with simple linear regression?
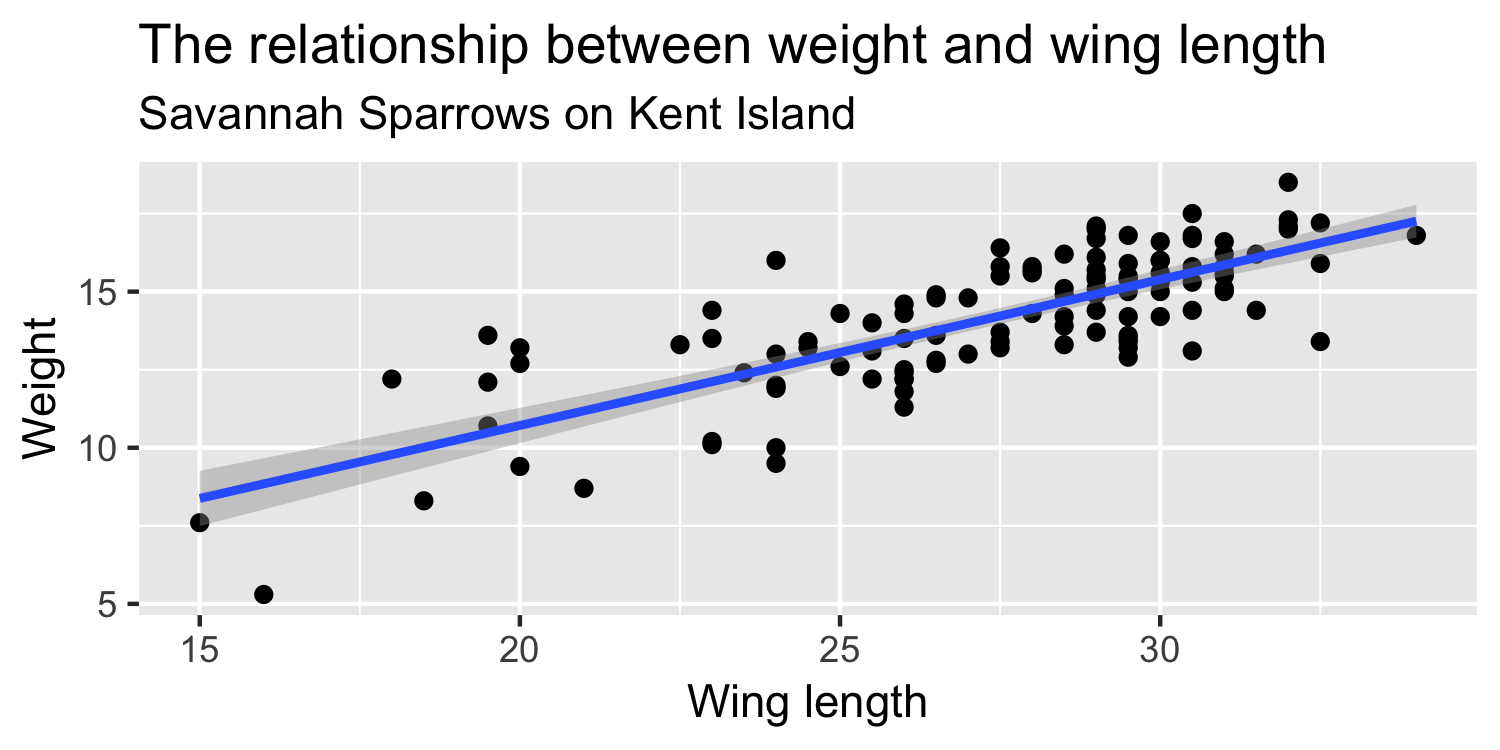
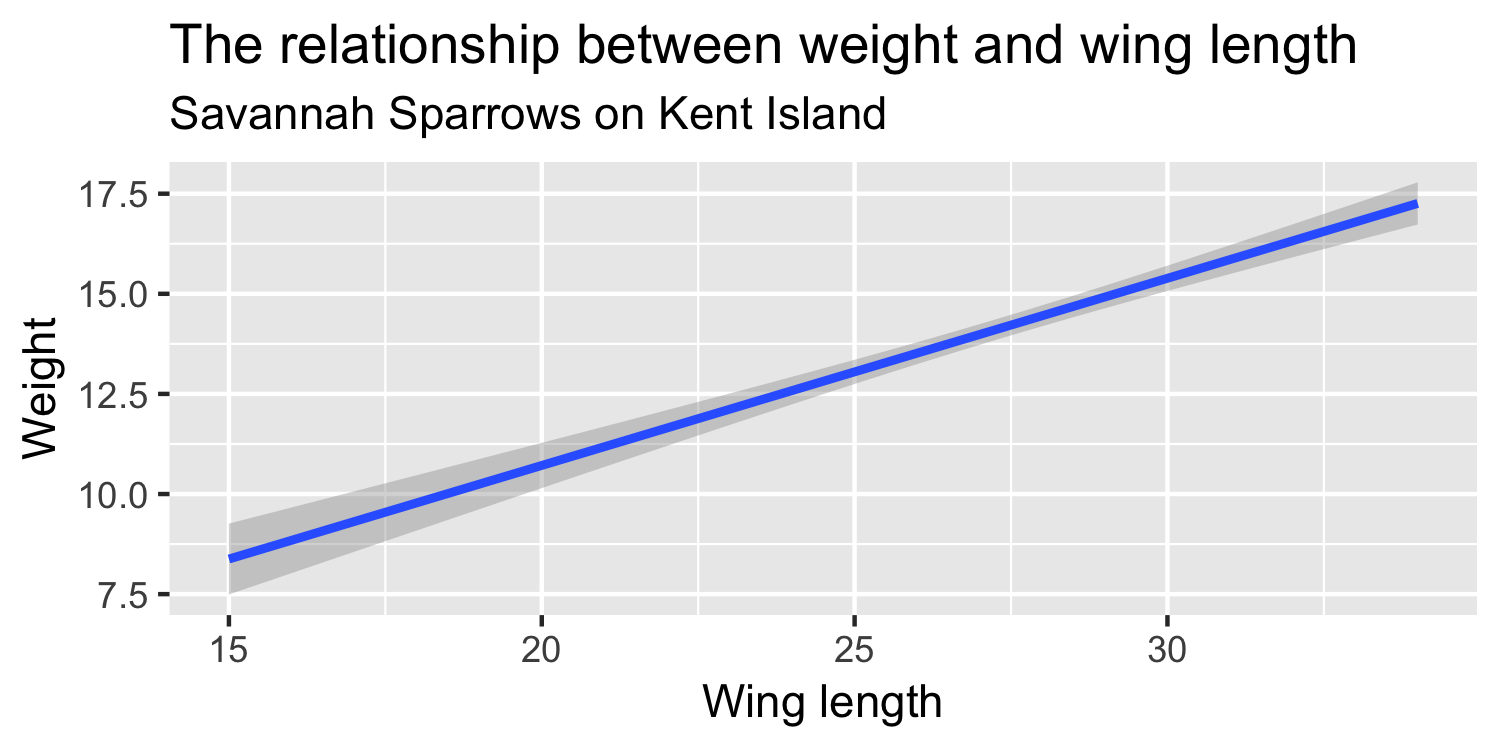
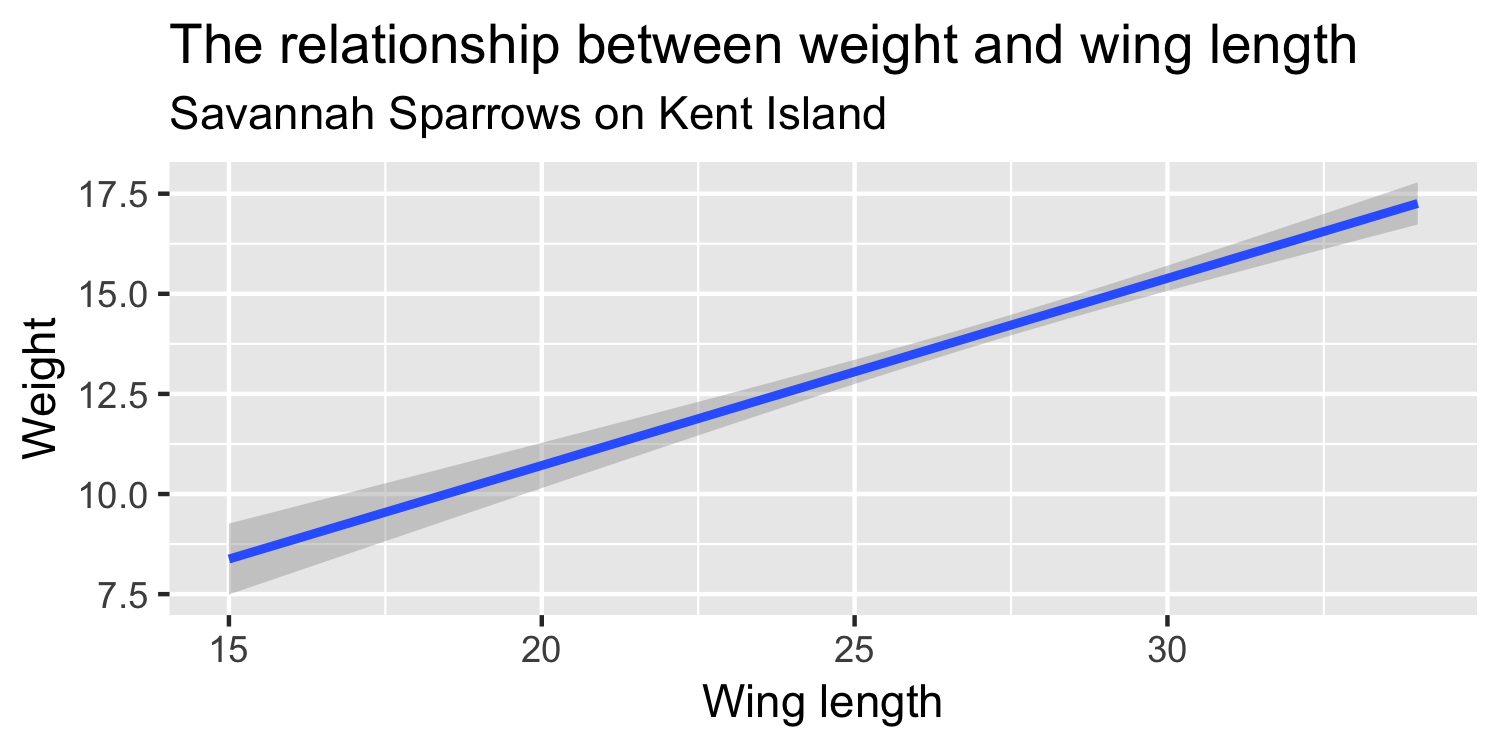
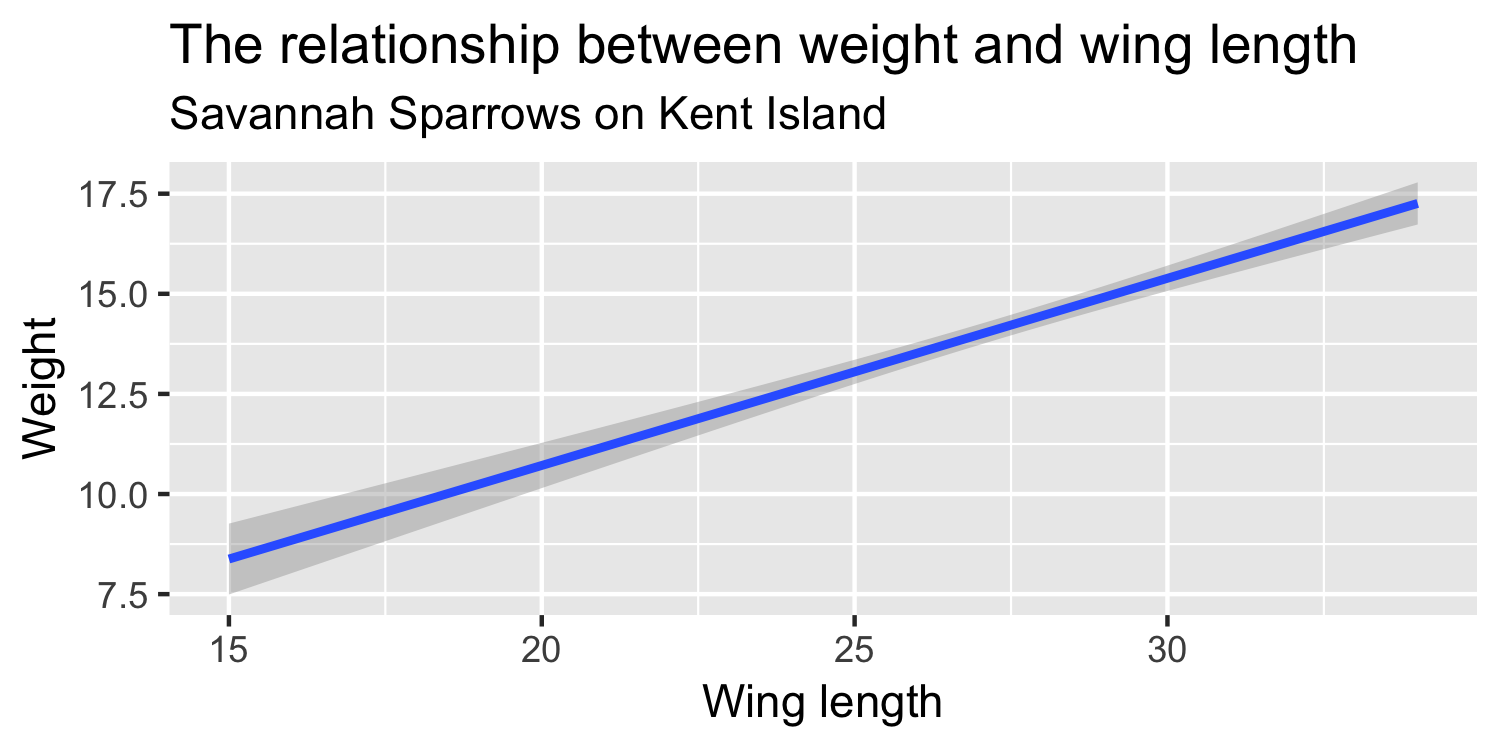
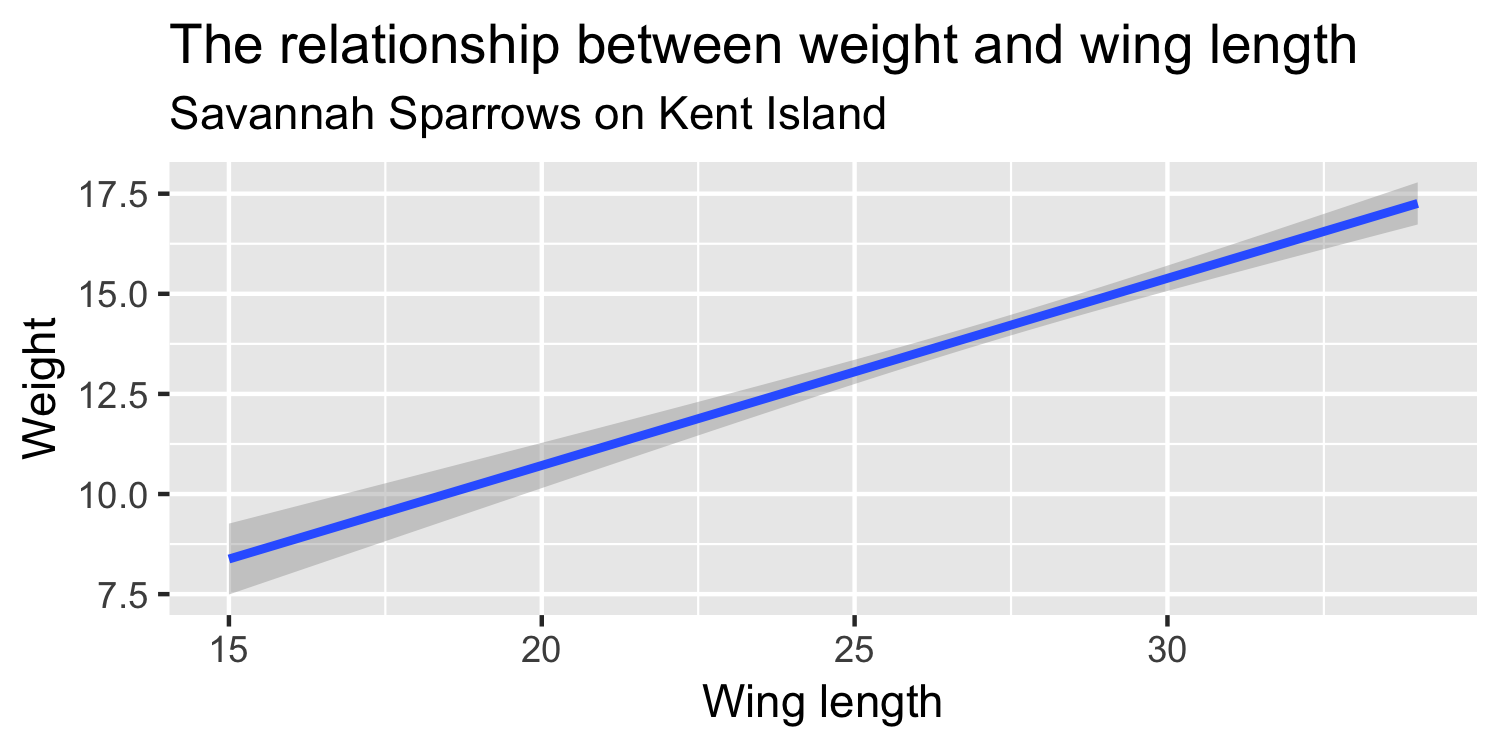
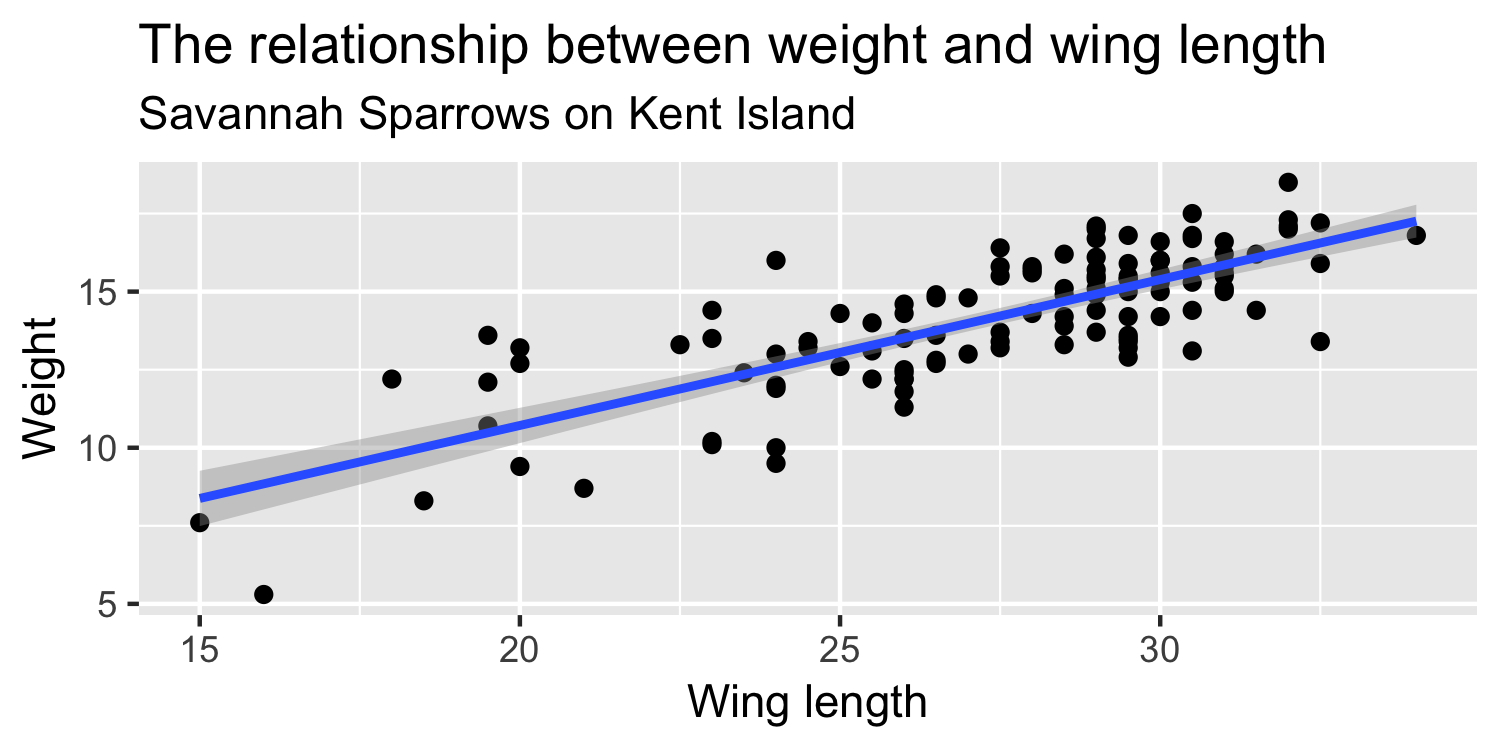
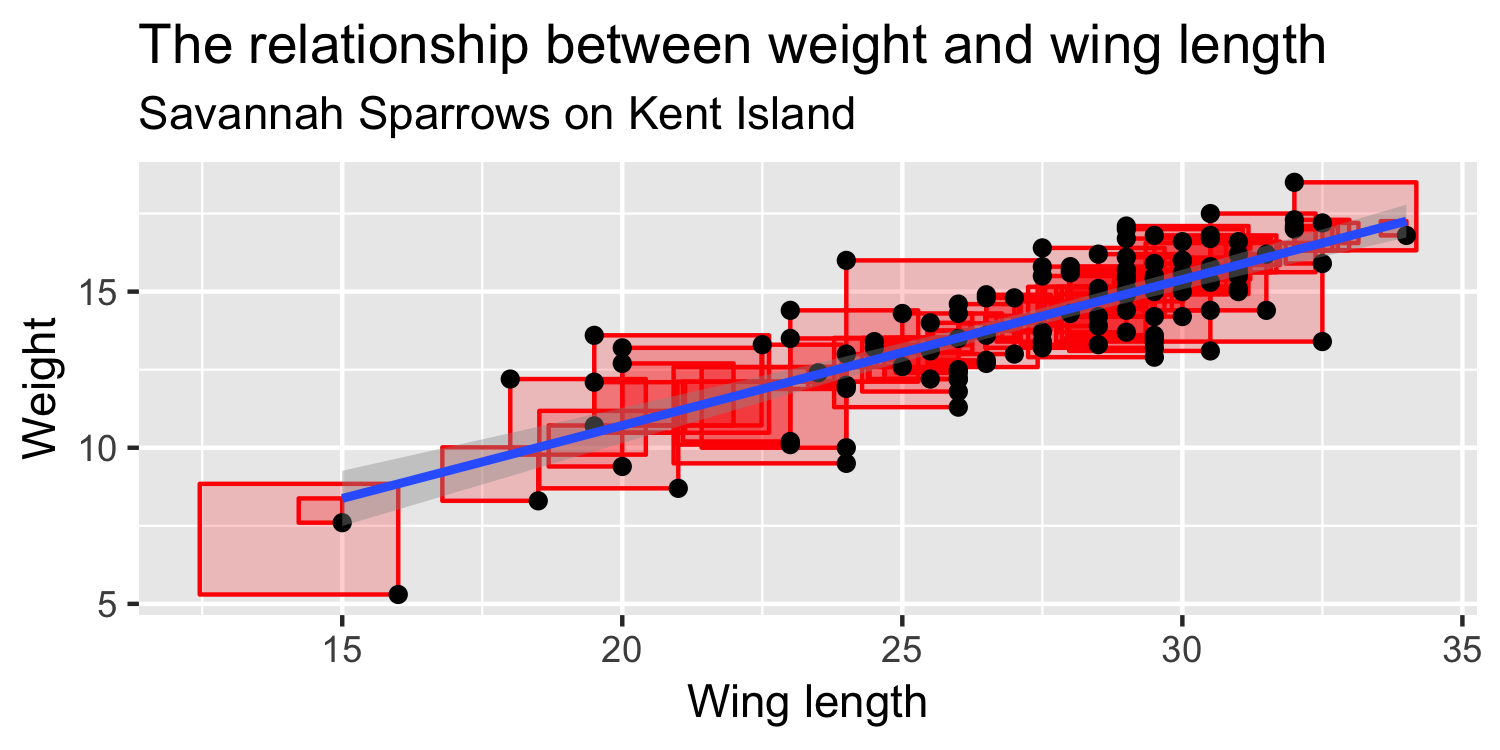
We express the mean weight of sparrows as a linear function of wing length.
What is the equation that represents this line?
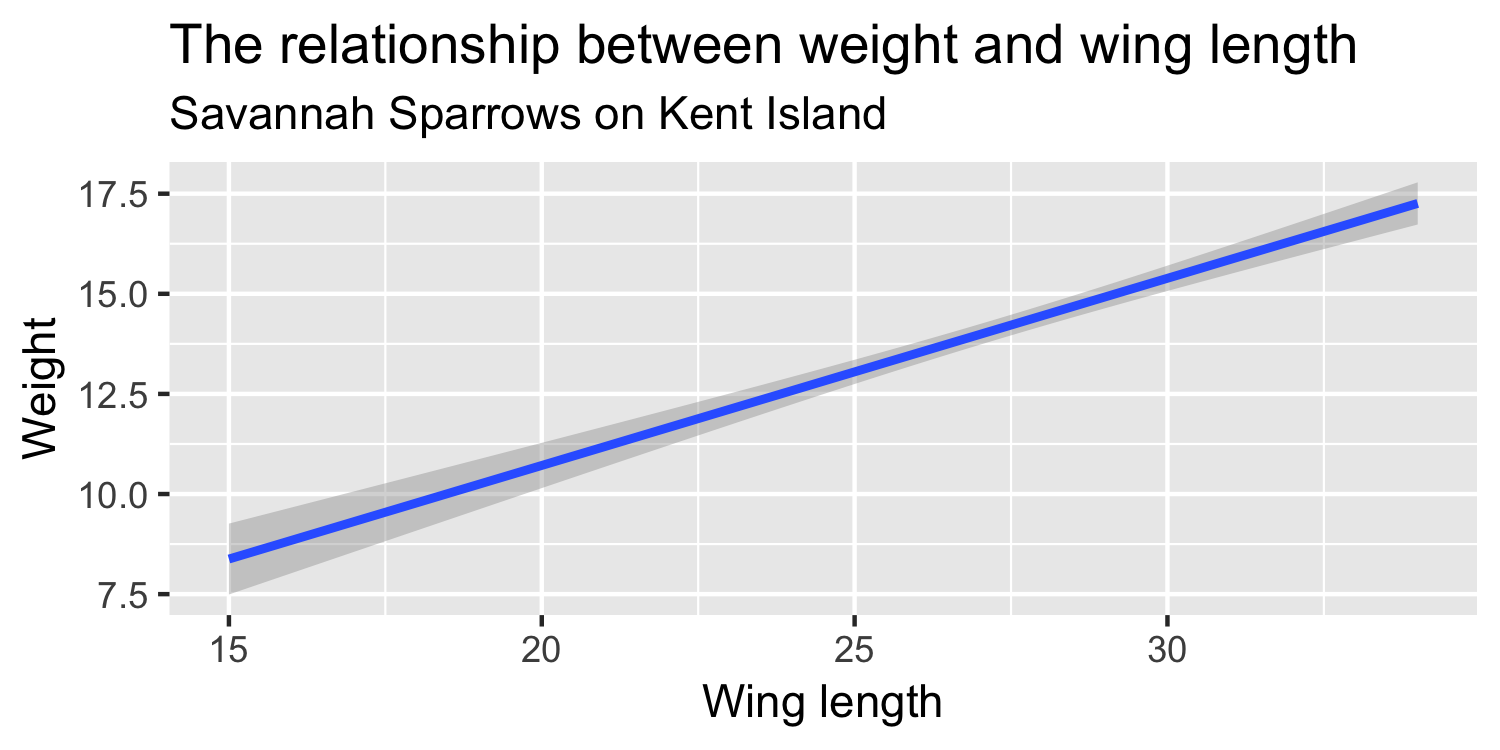
y = mx + b
y=β0+β1x
y=β0+β1×Wing Length
Weight=β0+β1×Wing Length
What is β0?
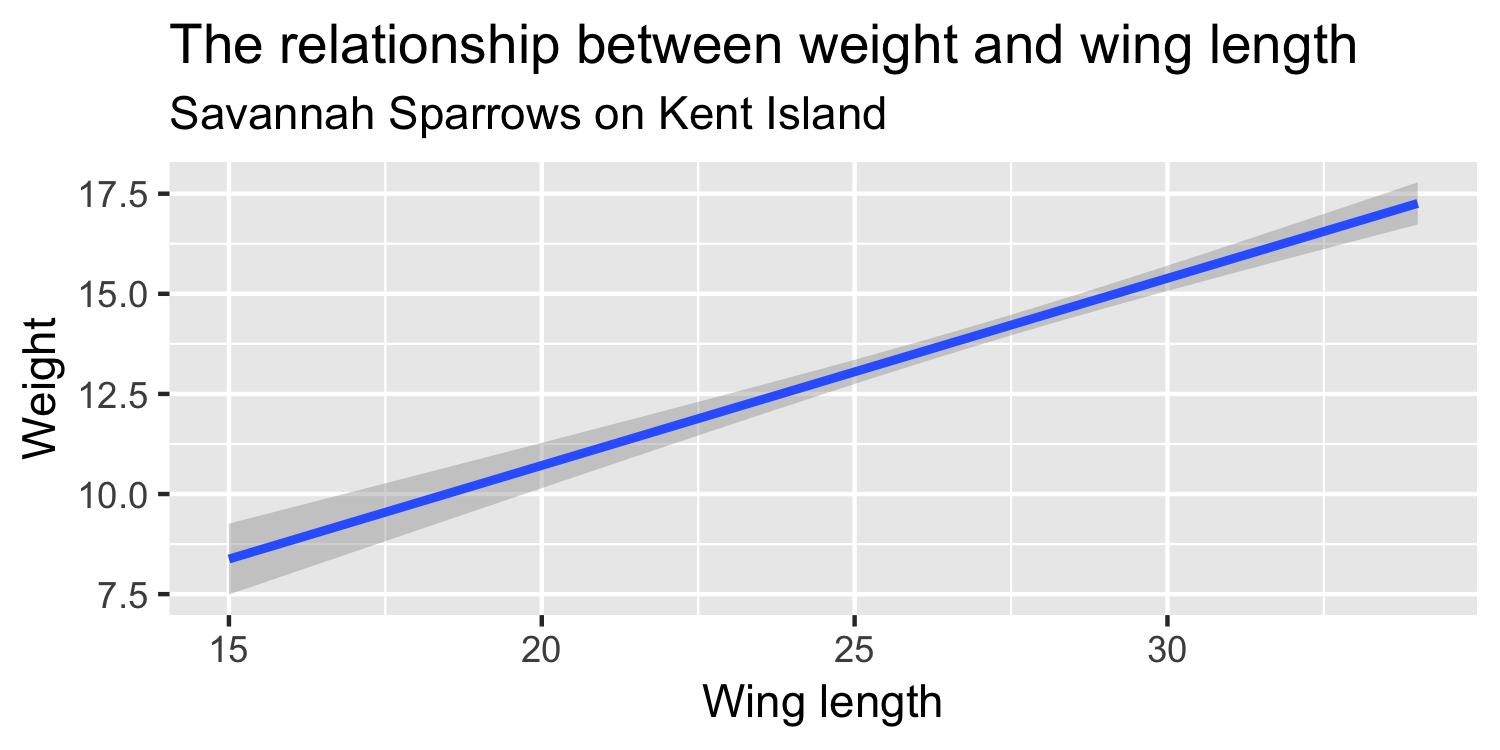
What is β0?
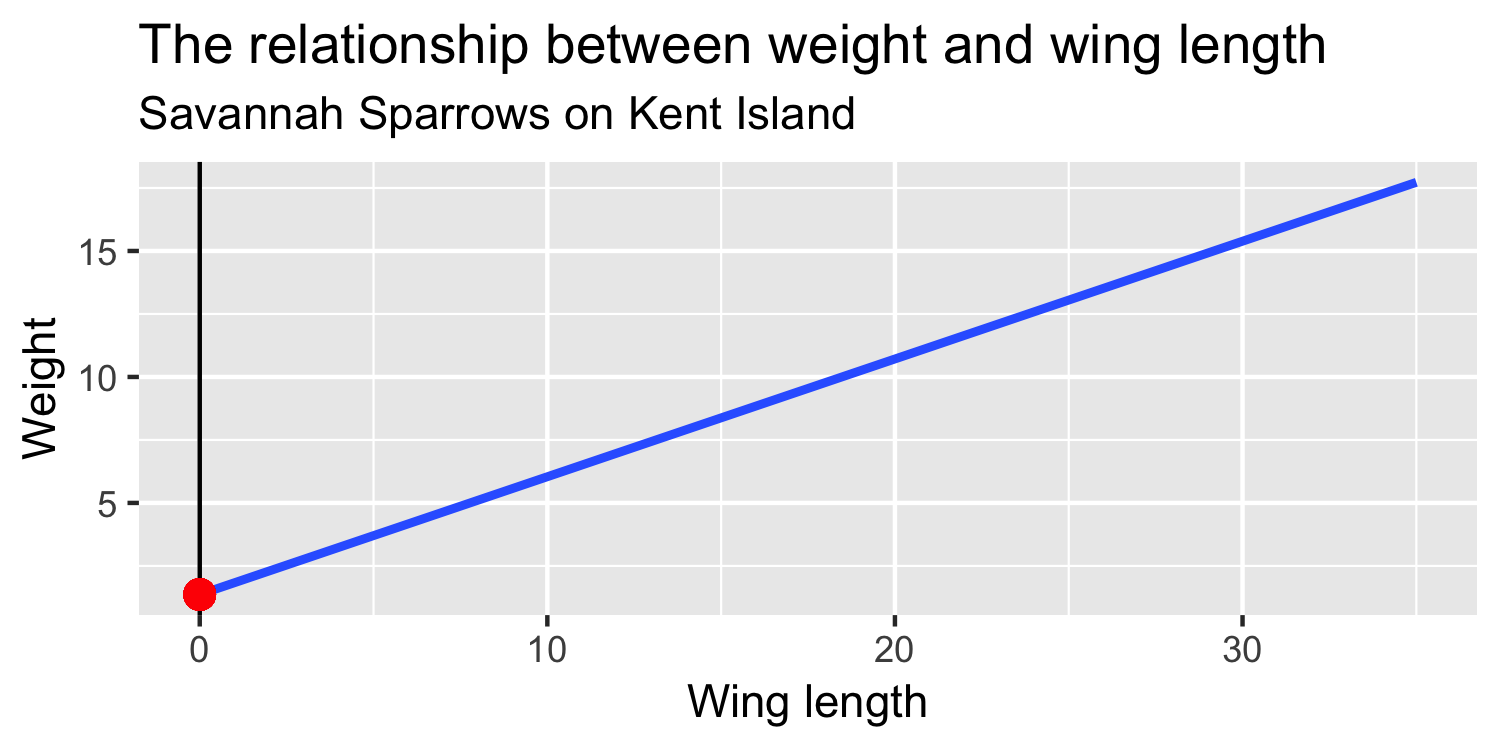
What is β1?
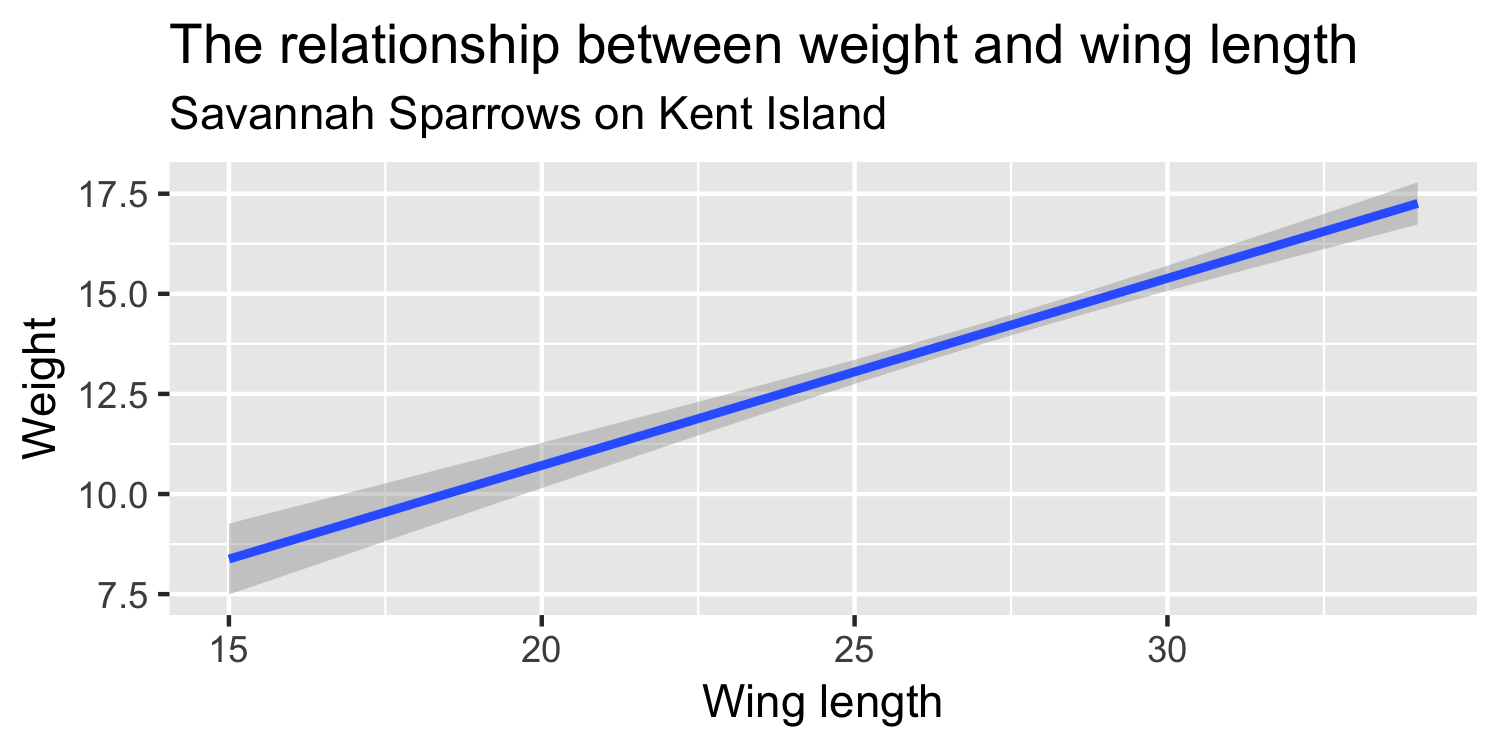
What is β1?
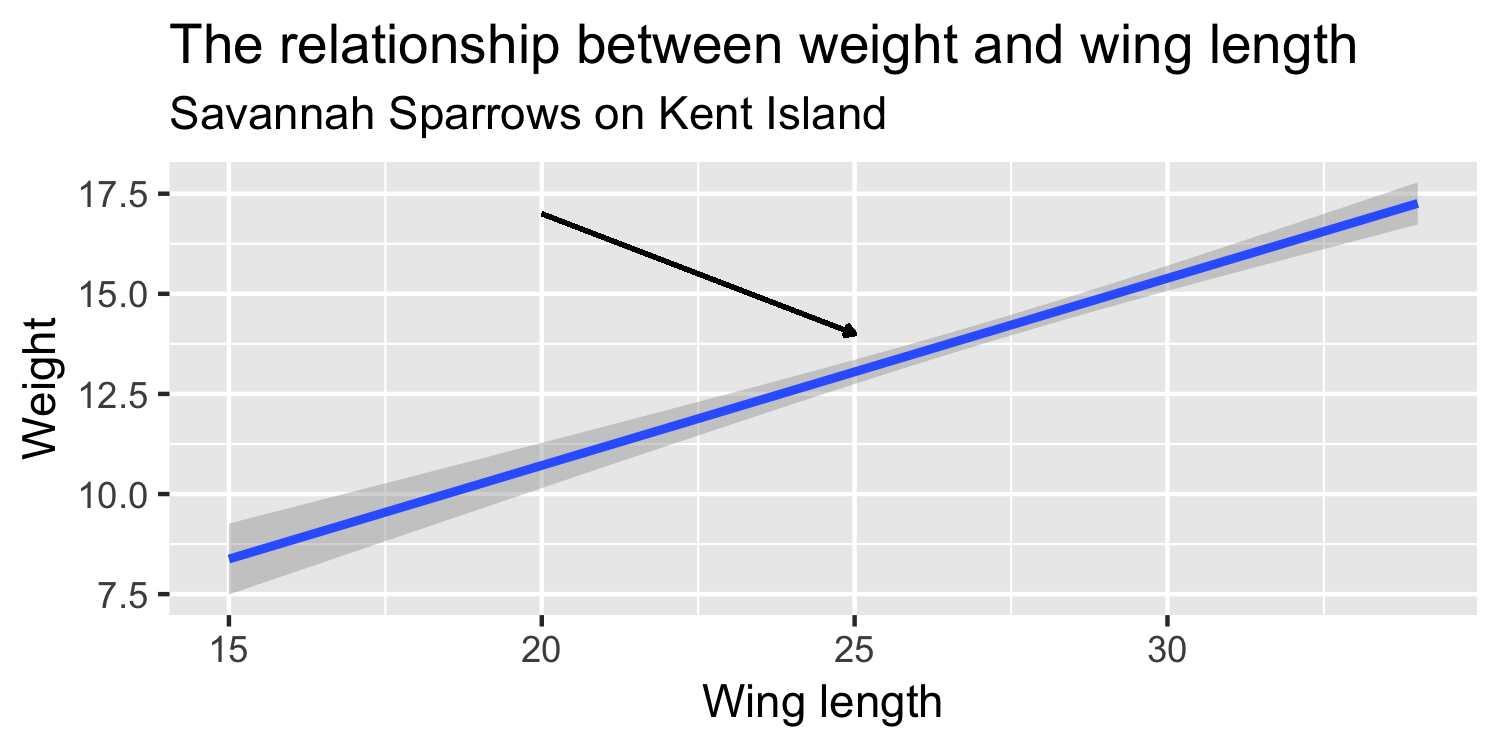
Do all of the data points actually fall exactly on the line?
y=β0+β1x+ϵ
y=β0+β1x+ϵ
y=β0+β1x+ϵ
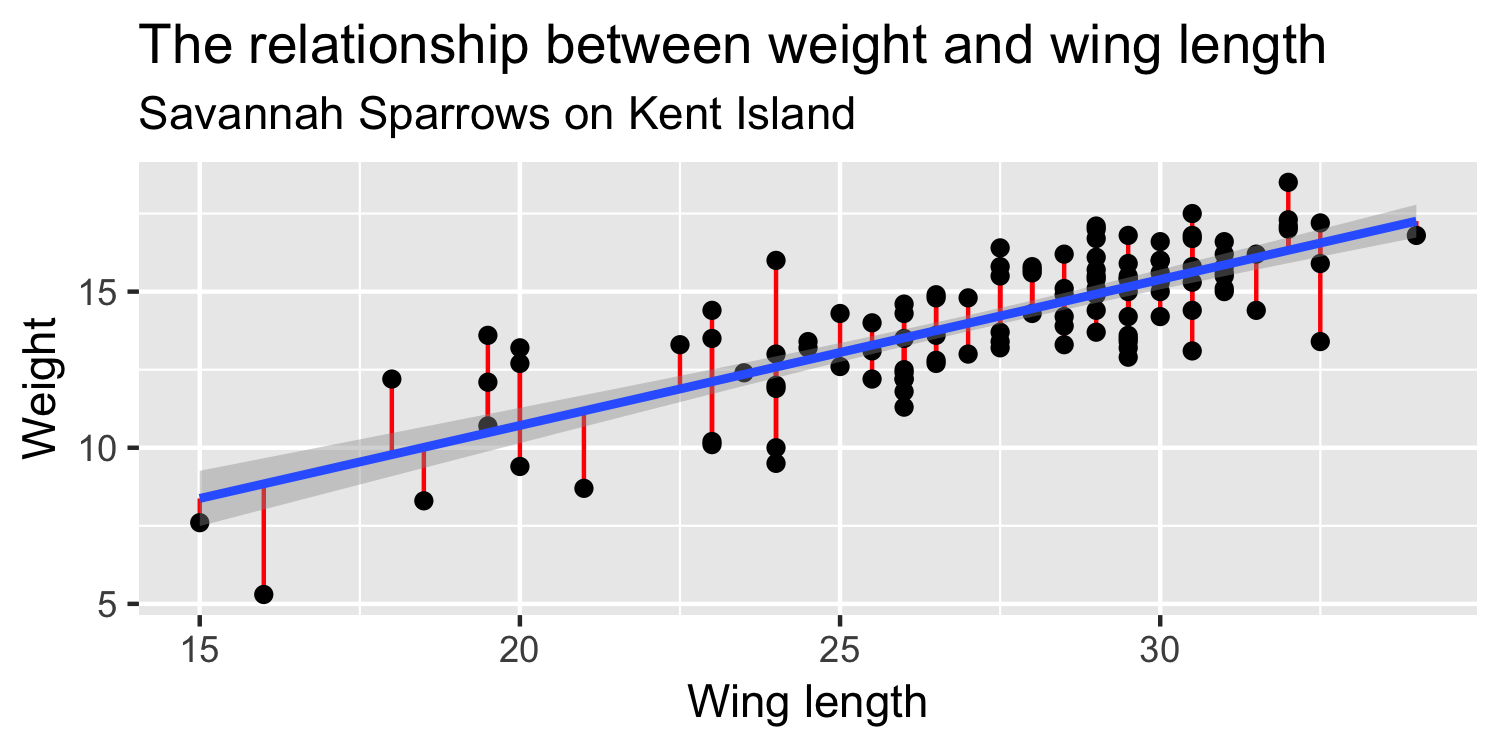
Truth
y=β0+β1x+ϵ

Truth
y=β0+β1x+ϵ
If we had the whole population of sparrows we could quantify the exact relationship between y and x
Reality
^y=^β0+^β1x

Reality
^y=^β0+^β1x
In reality, we have a sample of sparrows to estimate the relationship between x and y. The "hats" represent that these are estimated (fitted) values
Put a hat on it
How can you tell the difference between a parameter that is from the whole population versus a sample?

Pause for definitions
Definitions
- parameters
- β0
- β1
- population versus sample
- simple linear model
Definitions
- parameters: β0, β1
- β0: intercept
- β1: slope
- population versus sample
- simple linear model: y=β0+β1x+ϵ estimated by ^y=^β0+^β1x
Let's do this in R
library(Stat2Data)data(Sparrows)lm(Weight ~ WingLength, data = Sparrows)## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.4674What is ^β0?
lm(Weight ~ WingLength, data = Sparrows)## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.4674What is ^β1?
lm(Weight ~ WingLength, data = Sparrows)## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.4674y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict()y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat) %>% select(WingLength, y_hat) %>% slice(1:5)## WingLength y_hat## 1 29 14.92020## 2 31 15.85501## 3 25 13.05059## 4 29 14.92020## 5 30 15.38761Let's try to match these values using ^β0 and ^β1
## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.4674## WingLength y_hat## 1 29 14.92020## 2 31 15.85501## 3 25 13.05059## 4 29 14.92020## 5 30 15.38761lm(Weight ~ WingLength, data = Sparrows)## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.46741.365+0.4674×29
lm(Weight ~ WingLength, data = Sparrows)## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Coefficients:## (Intercept) WingLength ## 1.3655 0.46741.365+0.4674×29=14.92
How'd we do?
y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat) %>% select(WingLength, y_hat) %>% slice(1:5)## WingLength y_hat## 1 29 14.92020## 2 31 15.85501## 3 25 13.05059## 4 29 14.92020## 5 30 15.38761How did we decide on THIS line?
Minimizing Least Squares
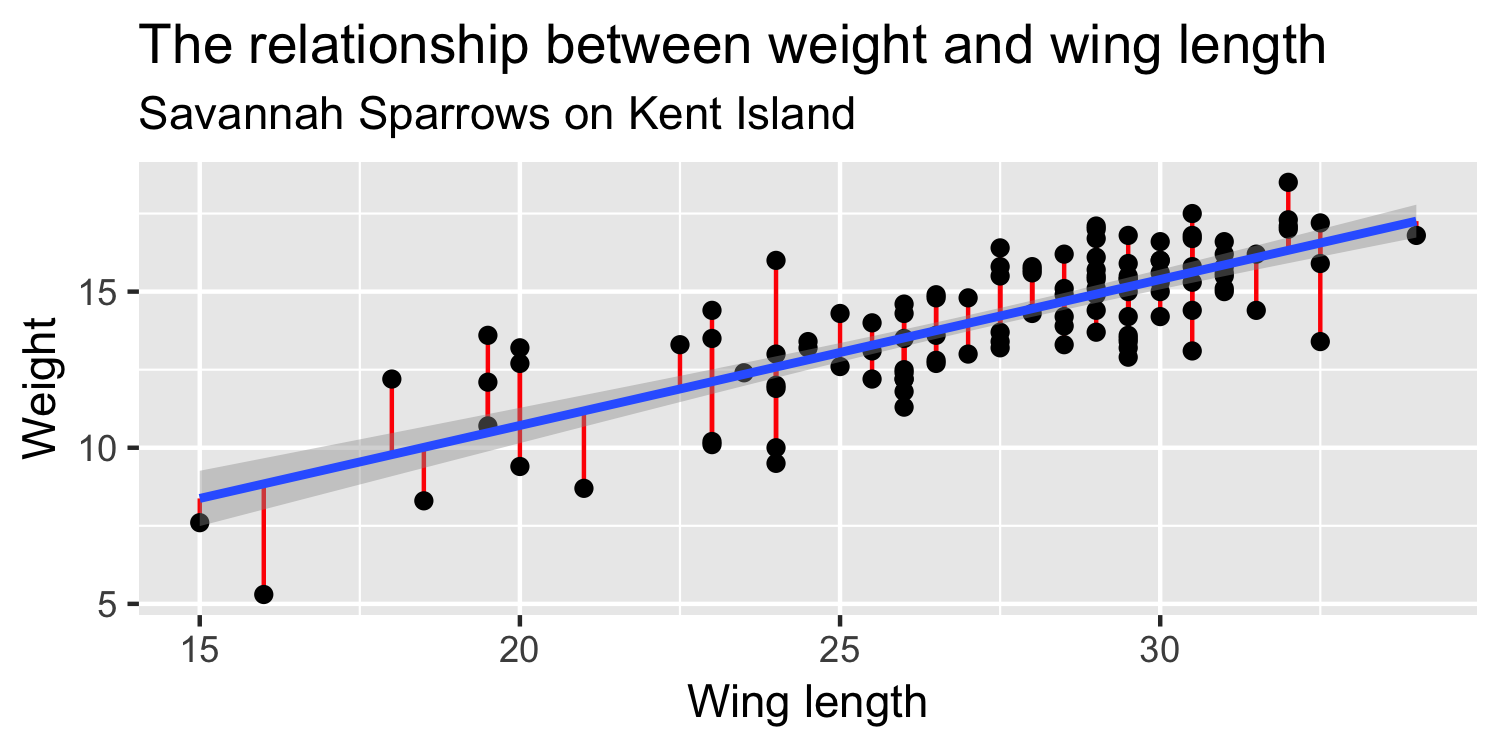
Minimizing Least Squares
Minimizing Least Squares
Minimizing Least Squares
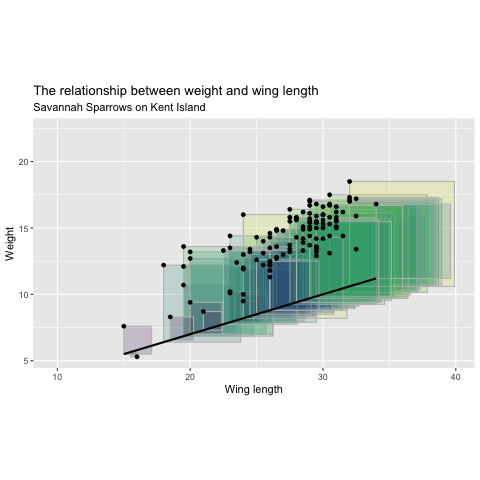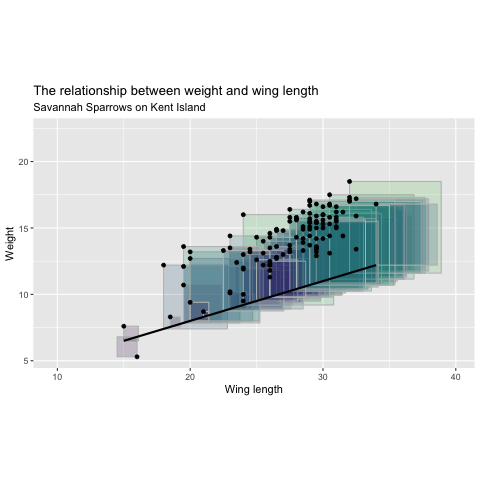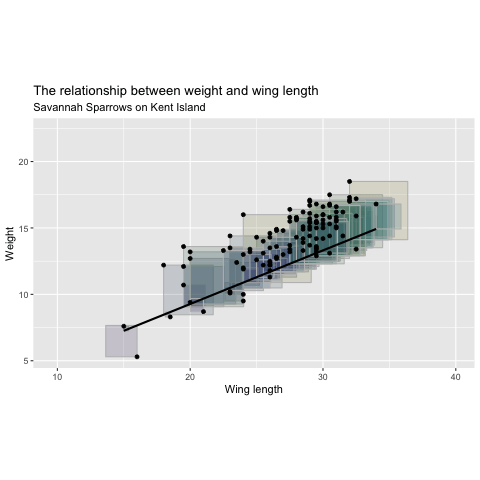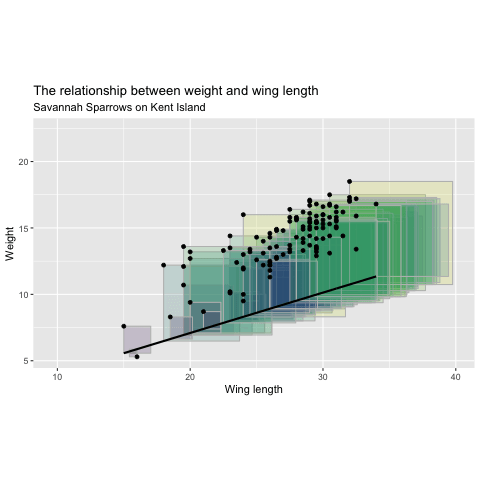
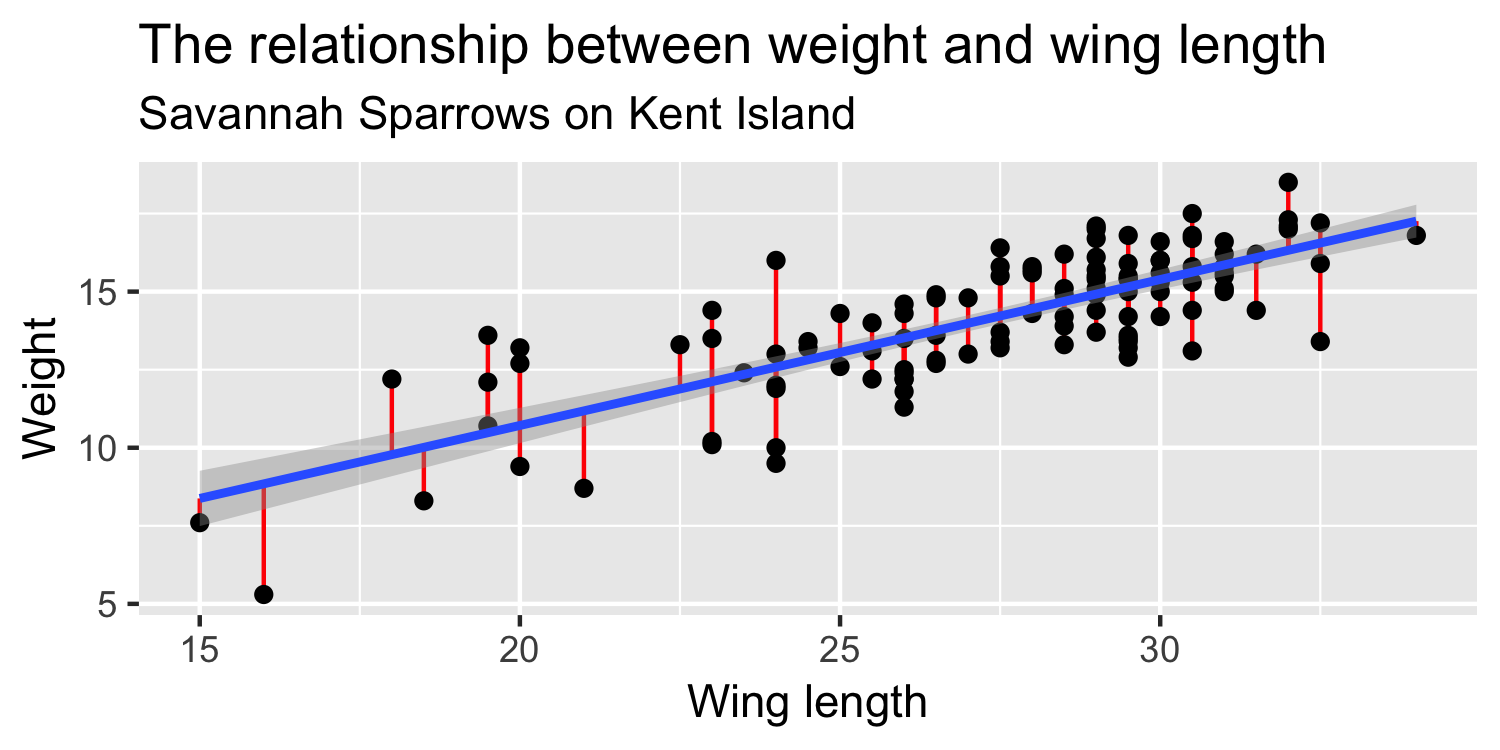
"Squared Residuals"
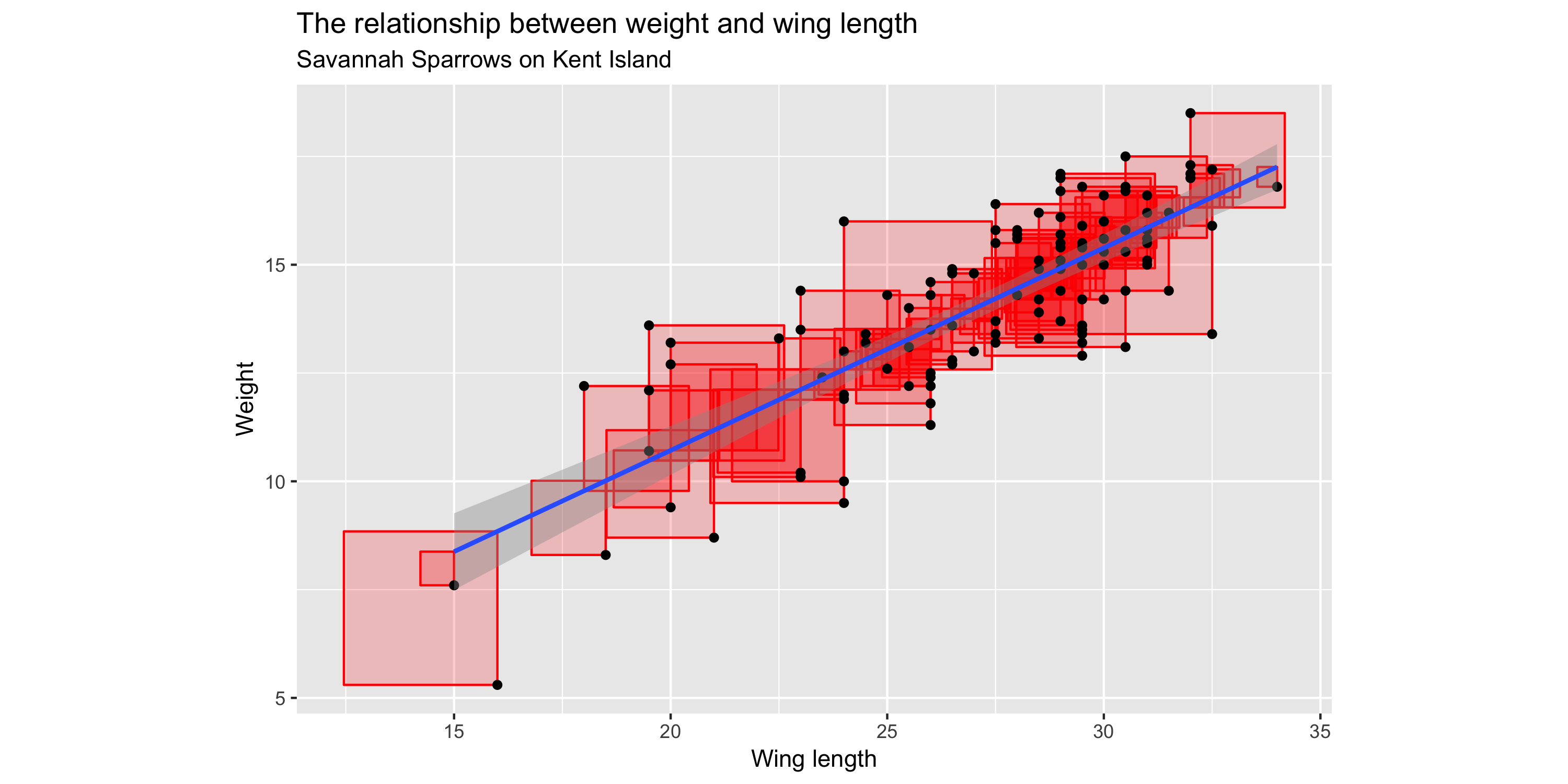
"Residuals"
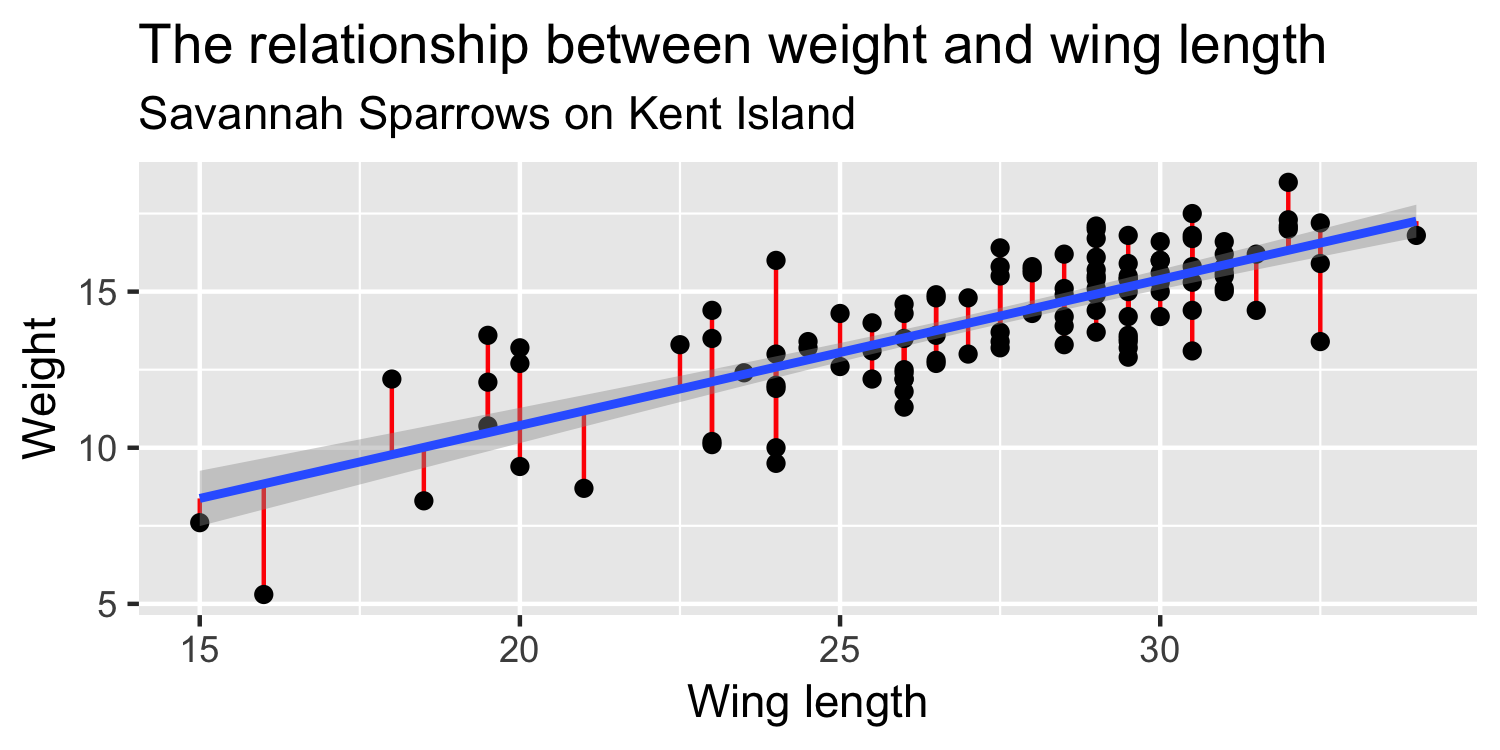
Definitions
- residual (e)
- squared residual (e2)
- sum of squared residual (SSE)
- standard deviation of the errors (σϵ)
- n
Definitions
- residual (e): observed y - predicted y → y−^y
Definitions
- residual (e): observed y - predicted y → y−^y
- squared residual (e2): (y−^y)2
Definitions
- residual (e): observed y - predicted y → y−^y
- squared residual (e2): (y−^y)2
- sum of squared residual (SSE): ∑(y−^y)2
Definitions
- residual (e): observed y - predicted y → y−^y
- squared residual (e2): (y−^y)2
- sum of squared residual (SSE): ∑(y−^y)2
- standard deviation of the errors (σϵ): estimated by ^σϵ=√SSEn−2 (regression standard error)
Definitions
- residual (e): observed y - predicted y → y−^y
- squared residual (e2): (y−^y)2
- sum of squared residual (SSE): ∑(y−^y)2
- standard deviation of the errors (σϵ): estimated by ^σϵ=√SSEn−2 (regression standard error)
- n: sample size
☝️ Note about notation
- ∑(y−^y)2
☝️ Note about notation
- ∑(y−^y)2
- ∑ni=1(yi−^yi)2
☝️ Note about notation
the i indicates for a single individual
ei=yi−^yi
☝️ Note about notation
for the first observation, i = 1
e1=y1−^y1
☝️ Note about notation
for the first observation, i = 1
−0.02=14.9−14.92
Back to R!
Calculate the residual
y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat, residual = Weight - y_hat) %>% select(Weight, y_hat, residual) %>% slice(1:5)## Weight y_hat residual## 1 14.9 14.92020 -0.02020496## 2 15.0 15.85501 -0.85501292## 3 14.3 13.05059 1.24941095## 4 17.0 14.92020 2.07979504## 5 16.0 15.38761 0.61239106Calculate the squared residuals
y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat, residual = Weight - y_hat, residual_2 = residual^2) %>% select(Weight, y_hat, residual, residual_2) %>% slice(1:5)## Weight y_hat residual residual_2## 1 14.9 14.92020 -0.02020496 0.0004082405## 2 15.0 15.85501 -0.85501292 0.7310470869## 3 14.3 13.05059 1.24941095 1.5610277150## 4 17.0 14.92020 2.07979504 4.3255474012## 5 16.0 15.38761 0.61239106 0.3750228116Calculate the SSE
y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat, residual = Weight - y_hat, residual_2 = residual^2) %>% summarise(sse = sum(residual_2))## sse## 1 223.3107Calculate the regression standard error
y_hat <- lm(Weight ~ WingLength, data = Sparrows) %>% predict() Sparrows %>% mutate(y_hat = y_hat, residual = Weight - y_hat, residual_2 = residual^2) %>% summarise(sse = sum(residual_2), n = n(), rse = sqrt(sse / (n - 2)))## sse n rse## 1 223.3107 116 1.399595Calculate the regression standard error
## sse n rse## 1 223.3107 116 1.399595lm(Weight ~ WingLength, data = Sparrows) %>% summary()## ## Call:## lm(formula = Weight ~ WingLength, data = Sparrows)## ## Residuals:## Min 1Q Median 3Q Max ## -3.5440 -0.9935 0.0809 1.0559 3.4168 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 1.36549 0.95731 1.426 0.156## WingLength 0.46740 0.03472 13.463 <2e-16## ## Residual standard error: 1.4 on 114 degrees of freedom## Multiple R-squared: 0.6139, Adjusted R-squared: 0.6105 ## F-statistic: 181.3 on 1 and 114 DF, p-value: < 2.2e-16 Porsche Price
- Go to RStudio Cloud and open
Porsche Price - For each question you work on, set the
evalchunk option toTRUEand knit
Linearity
The overall relationship between the variables has a linear pattern. The average values of the response y for each value of x fall on a common straight line.
Zero Mean
The error distribution is centered at zero. This means that the points are scattered at random above and below the line. (Note: By using least squares regression, we force the residual mean to be zero. Other techniques would not necessarily satisfy this condition.)
Constant Variance
The variability in the errors is the same for all values of the predictor variable. This means that the spread of points around the line remains fairly constant.
Independence
The errors are assumed to be independent from one another. Thus, one point falling above or below the line has no influence on the location of another point. When we are interested in using the model to make formal inferences (conducting hypothesis tests or providing confidence intervals), additional assumptions are needed.
Random
The data are obtained using a random process. Most commonly, this arises either from random sampling from a population of interest or from the use of randomization in a statistical experiment.
Normality
In order to use standard distributions for confidence intervals and hypothesis tests, we often need to assume that the random errors follow a normal distribution.
Summarise conditions
For a quantitative response variable y and a single quantitative explanatory variable x, the simple linear regression model is
y=β0+β1x+ϵ
where ϵ follows a normal distribution, that is, ϵ∼N(0,σϵ), and the errors are independent from one another.
broom


- You're familiar with the tidyverse:
library(tidyverse)- The broom package takes the messy output of built-in functions in R, such as
lm, and turns them into tidy data frames.
library(broom)## Warning: package 'broom' was built under R version 3.5.2 Porsche Price
- Go to RStudio Cloud and open
Porsche Price